Στοιχεία Εὐκλείδου β΄

[Βιβλίον II]

Αἱ Προτάσεις τῶν Στοιχείων β΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις

Πρότασις ζ΄. [7]

Ἐὰν εὐθεῖα γραμμή τμηθῇ, ὡς ἔτυχεν, τὸ ἀπὸ τῆς ὅλης καὶ τὸ ἀφ' ἑνὸς τῶν τμημάτων τὰ συναμφότερα τετράγωνα ἴσα ἐστὶ τῷ τε δὶς ὑπὸ τῆς ὅλης καὶ τοῦ εἰρημένου τμήματος περιεχομένῳ ὀρθογωνίῳ καὶ τῷ ἀπὸ τοῦ λοιποῦ τμήματος τετραγώνῳ.

Εὐθεῖα γάρ τις ἡ ΑΒ τετμήσθω, ὡς ἔτυχεν, κατὰ τὸ Γ σημεῖον· λέγω, ὅτι τὰ ἀπὸ τῶν ΑΒ, ΒΓ τετράγωνα ἴσα ἐστὶ τῷ τε δὶς ὑπὸ τῶν ΑΒ, ΒΓ περιεχόμενα ὀρθογωνίῳ καὶ τῷ ἀπὸ τῆς ΓΑ τετραγώνῳ. Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΑΒ τετράγωνον τὸ ΑΔΕΒ· καὶ καταγεγράφθω τὸ σχῆμα.

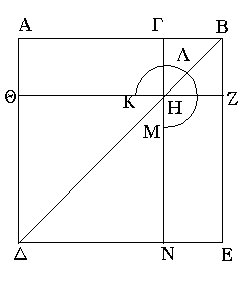
Ἐπεὶ οὖν ἴσον ἐστὶ τὸ ΑΗ τῷ ΗΕ, κοινὸν προσκείσθω τὸ ΓΖ· ὅλον ἄρα τὸ ΑΖ ὅλῳ τῷ ΓΕ ἴσον ἐστίν· τὰ ἄρα ΑΖ, ΓΕ διπλάσιά ἐστι τοῦ ΑΖ. ἀλλὰ τὰ ΑΖ, ΓΕ ὁ ΚΛΜ ἐστι γνώμων καὶ τὸ ΓΖ τετράγωνον· ὁ ΚΛΜ ἄρα γνώμων καὶ τὸ ΓΖ διπλάσιά ἐστι τοῦ ΑΖ. ἔστι δὲ τοῦ ΑΖ διπλάσιον καὶ τὸ δὶς ὑπὸ τῶν ΑΒ, ΒΓ· ἴση γὰρ ἡ ΒΖ τῇ ΒΓ· ὁ ἄρα ΚΛΜ γνώμων καὶ τὸ ΓΖ τετράγωνον ἴσον ἐστὶ τῷ δὶς ὑπὸ τῶν ΑΒ, ΒΓ. κοινὸν προσκείσθω τὸ ΔΗ, ὅ ἐστιν ἀπὸ τῆς ΑΓ τετράγωνον· ὁ ἄρα ΚΛΜ γνώμων καὶ τὰ ΒΗ, ΗΔ τετράγωνα ἴσα ἐστὶ τῷ τε δὶς ὑπὸ τῶν ΑΒ, ΒΓ περιεχομένῳ ὀρθογωνίῳ καὶ τῷ ἀπὸ τῆς ΑΓ τετραγώνῳ. ἀλλὰ ὁ ΚΛΜ γνώμων καὶ τὰ ΒΗ, ΗΔ τετράγωνα ὅλον ἐστὶ τὸ ΑΔΕΒ καὶ τὸ ΓΖ, ἅ ἐστιν ἀπὸ τῶν ΑΒ, ΒΓ τετράγωνα· τὰ ἄρα ἀπὸ τῶν ΑΒ, ΒΓ τετράγωνα ἴσα ἐστὶ τῷ [τε] δὶς ὑπὸ τῶν ΑΒ, ΒΓ περιεχομένῳ ὀρθογωνίῳ μετὰ τοῦ ἀπὸ τῆς ΑΓ τετραγώνου.

Ἐὰν ἄρα εὐθεῖα γραμμὴ τμηθῇ, ὡς ἔτυχεν, τὸ ἀπὸ τῆς ὅλης καὶ τὸ ἀφ’ ἑνὸς τῶν τμημάτων τὰ συναμφότερα ἴσα ἐστὶ τῷ τε δὶς ὑπὸ τῆς ὅλης καὶ τοῦ εἰρημένου τμήματος περιεχομένω ὀρθογωνίῳ καὶ τῷ ἀπὸ τοῦ λοιποῦ τμήματος τετραγώνῷ· ὅπερ ἔδει δεῖξαι.

Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων β΄.
Περιεχόμενα Στοιχείων Εὐκλείδου