Στοιχεία Εὐκλείδου ιβ΄
[Βιβλίον XII]
Αἱ Προτάσεις τῶν Στοιχείων ιβ΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις η΄. [8]
Αἱ ὅμοιαι πυραμίδες καὶ τριγώνους ἔχουσαι βάσεις ἐν τριπλασίονι λόγῳ εἰσὶ τῶν ὁμολόγων πλευρῶν.
Ἔστωσαν ὅμοιαι καὶ ὁμοίως κείμεναι πυραμίδες, ὧν βάσεις μέν εἰσι τὰ ΑΒΓ, ΔΕΖ τρίγωνα, κορυφαὶ δὲ τὰ Η, Θ σημεῖα· λέγω, ὅτι ἡ ΑΒΓΗ πυραμὶς πρὸς τὴν ΔΕΖΘ πυραμίδα τριπλασίονα λόγον ἔχει ἤπερ ἡ ΒΓ πρὸς τὴν ΕΖ.
Συμπεπληρώσθω γὰρ τὰ ΒΗΜΛ, ΕΘΠΟ στερεὰ παραλληλεπίπεδα. καὶ ἐπεὶ ὁμοία ἐστὶν ἡ ΑΒΓΗ πυραμὶς τῇ ΔΕΖΘ πυραμίδι, ἴση ἄρα ἐστὶν ἡ μὲν ὑπὸ ΑΒΓ γωνία τῇ ὑπὸ ΔΕΖ γωνίᾳ, ἡ δὲ ὑπὸ ΗΒΓ τῇ ὑπὸ ΘΕΖ, ἡ δὲ ὑπὸ ΑΒΗ τῇ ὑπὸ ΔΕΘ, καί ἐστιν ὡς ἡ ΑΒ πρὸς τὴν ΔΕ, οὕτως ἡ ΒΓ πρὸς τὴν ΕΖ, καὶ ἡ ΒΗ πρὸς τὴν ΕΘ. καὶ ἐπεί ἐστιν ὡς ἡ ΑΒ πρὸς τὴν ΔΕ, οὕτως ἡ ΒΓ πρὸς τὴν ΕΖ, καὶ περὶ ἴσας γωνίας αἱ πλευραὶ ἀνάλογόν εἰσιν, ὅμοιον ἄρα ἐστὶ τὸ ΒΜ παραλληλόγραμμον τῷ ΕΠ παραλληλογράμμῳ.
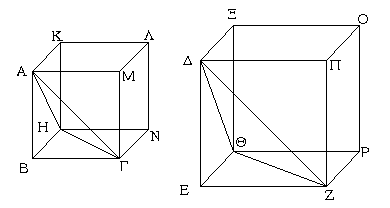
διὰ τὰ αὐτὰ δὴ καὶ τὸ μὲν ΒΝ τῷ ΕΡ ὅμοιόν ἐστι, τὸ δὲ ΒΚ τῷ ΕΞ· τὰ τρία ἄρα τὰ ΜΒ, ΒΚ, ΒΝ τρισὶ τοῖς ΕΠ, ΕΞ, ΕΡ ὅμοιά ἐστιν. ἀλλὰ τὰ μὲν τρία τὰ ΜΒ, ΒΚ, ΒΝ τρισὶ τοῖς ἀπεναντίον ἴσα τε καὶ ὅμοιά ἐστιν, τὰ δὲ τρία τὰ ΕΠ, ΕΞ, ΕΡ τρισὶ τοῖς ἀπεναντίον ἴσα τε καὶ ὅμοιά ἐστιν. τὰ ΒΗΜΛ, ΕΘΠΟ ἄρα στερεὰ ὑπὸ ὁμοίων ἐπιπέδων ἴσων τὸ πλῆθος περιέχεται. ὅμοιον ἄρα ἐστὶ τὸ ΒΗΜΛ στερεὸν τῷ ΕΘΠΟ στερεῷ. τὰ δὲ ὅμοια στερεὰ παραλληλεπίπεδα ἐν τριπλασίονι λόγῳ ἐστὶ τῶν ὁμολόγων πλευρῶν. τὸ ΒΗΜΛ ἄρα στερεὸν πρὸς τὸ ΕΘΠΟ στερεὸν τριπλασίονα λόγον ἔχει ἤπερ ἡ ὁμόλογος πλευρὰ ἡ ΒΓ πρὸς τὴν ὁμόλογον πλευρὰν τὴν ΕΖ. ὡς δὲ τὸ ΒΗΜΛ στερεὸν πρὸς τὸ ΕΘΠΟ στερεόν, οὕτως ἡ ΑΒΓΗ πυραμὶς πρὸς τὴν ΔΕΖΘ πυραμίδα, ἐπειδήπερ ἡ πυραμὶς ἕκτον μέρος ἐστὶ τοῦ στερεοῦ διὰ τὸ καὶ τὸ πρίσμα ἥμισυ ὂν τοῦ στερεοῦ παραλληλεπιπέδου τριπλάσιον εἶναι τῆς πυραμίδος. καὶ ἡ ΑΒΓΗ ἄρα πυραμὶς πρὸς τὴν ΔΕΖΘ πυραμίδα τριπλασίονα λόγον ἔχει ἤπερ ἡ ΒΓ πρὸς τὴν ΕΖ· ὅπερ ἔδει δεῖξαι.
Ἐκ δὴ τούτου φανερόν, ὅτι καὶ αἱ πολυγώνους ἔχουσαι βάσεις ὅμοιαι πυραμίδες πρὸς ἀλλήλας ἐν τριπλασίονι λόγῳ εἰσὶ τῶν ὁμολόγων πλευρῶν. διαιρεθεισῶν γὰρ αὐτῶν εἰς τὰς ἐν αὐταῖς πυραμίδας τριγώνους βάσεις ἐχούσας τῷ καὶ τὰ ὅμοια πολύγωνα τῶν βάσεων εἰς ὅμοια τρίγωνα διαιρεῖσθαι καὶ ἴσα τῷ πλήθει καὶ ὁμόλογα τοῖς ὅλοις ἔσται ὡς [ἡ] ἐν τῇ ἑτέρᾳ μία πυραμὶς τρίγωνον ἔχουσα βάσιν πρὸς τὴν ἐν τῇ ἑτέρᾳ μίαν πυραμίδα τρίγωνον ἔχουσαν βάσιν, οὕτως καὶ ἅπασαι αἱ ἐν τῇ ἑτέρᾳ πυραμίδι πυραμίδες τριγώνους ἔχουσαι βάσεις πρὸς τὰς ἐν τῇ ἑτέρᾳ πυραμίδι πυραμίδας τριγώνους βάσεις ἐχούσας, τουτέστιν αὐτὴ ἡ πολύγωνον βάσιν ἔχουσα πυραμὶς πρὸς τὴν πολύγωνον βάσιν ἔχουσαν πυραμίδα. ἡ δὲ τρίγωνον βάσιν ἔχουσα πυραμὶς πρὸς τὴν τρίγωνον βάσιν ἔχουσαν ἐν τριπλασίονι λόγῳ ἐστὶ τῶν ὁμολόγων πλευρῶν· καὶ ἡ πολύγωνον ἄρα βάσιν ἔχουσα πρὸς τὴν ὁμοίαν βάσιν ἔχουσαν τριπλασίονα λόγον ἔχει ἤπερ ἡ πλευρὰ πρὸς τὴν πλευράν.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ιβ΄.
Περιεχόμενα Στοιχείων Εὐκλείδου
Copyright©1999 Dimitrios E. Mourmouras