Στοιχεία Εὐκλείδου γ΄

[Βιβλίον III]

Αἱ Προτάσεις τῶν Στοιχείων γ΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις

Πρότασις ζ΄. [7]

Ἐὰν κύκλου ἐπὶ τῆς διαμέτρου ληφθῇ τι σημεῖον, ὃ μή ἐστι κέντρον τοῦ κύκλου, ἀπὸ δὲ τοῦ σημείου πρὸς τὸν κύκλον προσπίπτωσιν εὐθεῖαί τινες, μεγίστη μὲν ἔσται, ἐφ' ἧς τὸ κέντρον, ἐλαχίστη δὲ ἡ λοιπή, τῶν δὲ ἄλλων ἀεὶ ἡ ἔγγιον τῆς διὰ τοῦ κέντρου τῆς ἀπώτερον μείζων ἐστίν, δύο δὲ μόνον ἴσαι ἀπὸ τοῦ σημείου προσπεσοῦνται πρὸς τὸν κύκλον ἐφ' ἑκάτερα τῆς ἐλαχίστης.

Ἔστω κύκλος ὁ ΑΒΓΔ, διάμετρος δὲ αὐτοῦ ἔστω ἡ ΑΔ, καὶ ἐπὶ τῆς ΑΔ εἰλήφθω τι σημεῖον τὸ Ζ, ὃ μή ἐστι κέντρον τοῦ κύκλου, κέντρον δὲ τοῦ κύκλου ἔστω τὸ Ε, καὶ ἀπὸ τοῦ Ζ πρὸς τὸν ΑΒΓΔ κύκλον προσπιπτέτωσαν εὐθεῖαί τινες αἱ ΖΒ, ΖΓ, ΖΗ· λέγω, ὅτι μεγίστη μέν ἐστιν ἡ ΖΑ, ἐλαχίστη δὲ ἡ ΖΔ, τῶν δὲ ἄλλων ἡ μὲν ΖΒ τῆς ΖΓ μείζων, ἡ δὲ ΖΓ τῆς ΖΗ.

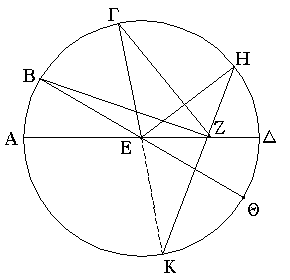
Ἐπεζεύχθωσαν γὰρ αἱ ΒΕ, ΓΕ, ΗΕ. καὶ ἐπεὶ παντὸς τριγώνου αἱ δύο πλευραὶ τῆς λοιπῆς μείζονές εἰσιν, αἱ ἄρα ΕΒ, ΕΖ τῆς ΒΖ μείζονές εἰσιν. ἴση δὲ ἡ ΑΕ τῇ ΒΕ [αἱ ἄρα ΒΕ, ΕΖ ἴσαι εἰσὶ τῇ ΑΖ]· μείζων ἄρα ἡ ΑΖ τῆς ΒΖ. πάλιν, ἐπεὶ ἴση ἐστὶν ἡ ΒΕ τῇ ΓΕ, κοινὴ δὲ ἡ ΖΕ, δύο δὴ αἱ ΒΕ, ΕΖ δυσὶ ταῖς ΓΕ, ΕΖ ἴσαι εἰσίν. ἀλλὰ καὶ γωνία ἡ ὑπὸ ΒΕΖ γωνίας τῆς ὑπὸ ΓΕΖ μείζων. βάσις ἄρα ἡ ΒΖ βάσεως τῆς ΓΖ μείζων ἐστίν. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΓΖ τῆς ΖΗ μείζων ἐστίν.

Πάλιν, ἐπεὶ αἱ ΗΖ, ΖΕ τῆς ΕΗ μείζονές εἰσιν, ἴση δὲ ἡ ΕΗ τῇ ΕΔ, αἱ ἄρα ΗΖ, ΖΕ τῆς ΕΔ μείζονές εἰσιν. κοινὴ ἀφῃρήσθω ἡ ΕΖ· λοιπὴ ἄρα ἡ ΗΖ λοιπῆς τῆς ΖΔ μείζων ἐστίν. μεγίστη μὲν ἄρα ἡ ΖΑ, ἐλαχίστη δὲ ἡ ΖΔ, μείζων δὲ ἡ μὲν ΖΒ τῆς ΖΓ, ἡ δὲ ΖΓ τῆς ΖΗ.

Λέγω, ὅτι καὶ ἀπὸ τοῦ Ζ σημείου δύο μόνον ἴσαι προσπεσοῦνται πρὸς τὸν ΑΒΓΔ κύκλον ἐφ' ἑκάτερα τῆς ΖΔ ἐλαχίστης. συνεστάτω γὰρ πρὸς τῇ ΕΖ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Ε τῇ ὑπὸ ΗΕΖ γωνίᾳ ἴση ἡ ὑπὸ ΖΕΘ, καὶ ἐπεζεύχθω ἡ ΖΘ. ἐπεὶ οὖν ἴση ἐστὶν ἡ ΗΕ τῇ ΕΘ, κοινὴ δὲ ἡ ΕΖ, δύο δὴ αἱ ΗΕ, ΕΖ δυσὶ ταῖς ΘΕ, ΕΖ ἴσαι εἰσίν· καὶ γωνία ἡ ὑπὸ ΗΕΖ γωνίᾳ τῇ ὑπὸ ΘΕΖ ἴση· βάσις ἄρα ἡ ΖΗ βάσει τῇ ΖΘ ἴση ἐστίν. λέγω δή, ὅτι τῇ ΖΗ ἄλλη ἴση οὐ προσπεσεῖται πρὸς τὸν κύκλον ἀπὸ τοῦ Ζ σημείου. εἰ γὰρ δυνατόν, προσπιπτέτω ἡ ΖΚ. καὶ ἐπεὶ ἡ ΖΚ τῇ ΖΗ ἴση ἐστίν, ἀλλὰ ἡ ΖΘ τῇ ΖΗ [ἴση ἐστίν], καὶ ἡ ΖΚ ἄρα τῇ ΖΘ ἐστιν ἴση, ἡ ἔγγιον τῆς διὰ τοῦ κέντρου τῇ ἀπώτερον ἴση· ὅπερ ἀδύνατον. οὐκ ἄρα ἀπὸ τοῦ Ζ σημείου ἑτέρα τις προσπεσεῖται πρὸς τὸν κύκλον ἴση τῇ ΗΖ· μία ἄρα μόνη.

Ἐὰν ἄρα κύκλου ἐπὶ τῆς διαμέτρου ληφθῇ τι σημεῖον, ὃ μή ἐστι κέντρον τοῦ κύκλου, ἀπὸ δὲ τοῦ σημείου πρὸς τὸν κύκλον προσπίπτωσιν εὐθεῖαί τινες, μεγίστη μὲν ἔσται, ἐφ' ἧς τὸ κέντρον, ἐλαχίστη δὲ ἡ λοιπή, τῶν δὲ ἄλλων ἀεὶ ἡ ἔγγιον τῆς διὰ τοῦ κέντρου τῆς ἀπώτερον μείζων ἐστίν, δύο δὲ μόνον ἴσαι ἀπὸ τοῦ αὐτοῦ σημείου προσπεσοῦνται πρὸς τὸν κύκλον ἐφ' ἑκάτερα τῆς ἐλαχίστης· ὅπερ ἔδει δεῖξαι.

Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων γ΄.
Περιεχόμενα Στοιχείων Εὐκλείδου