Στοιχεία Εὐκλείδου ζ΄
[Βιβλίον VII]
Αἱ Προτάσεις τῶν Στοιχείων ζ΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις γ΄. [3]
Τριῶν ἀριθμῶν δοθέντων μὴ πρώτων πρὸς ἀλλήλους τὸ μέγιστον αὐτῶν κοινὸν μέτρον εὑρεῖν.
Ἔστωσαν οἱ δοθέντες τρεῖς ἀριθμοὶ μὴ πρῶτοι πρὸς ἀλλήλους οἱ Α, Β, Γ· δεῖ δὴ τῶν Α, Β, Γ τὸ μέγιστον κοινὸν μέτρον εὑρεῖν.
Εἰλήφθω γὰρ δύο τῶν Α, Β τὸ μέγιστον κοινὸν μέτρον ὁ Δ· ὁ δὴ Δ τὸν Γ ἤτοι μετρεῖ ἢ οὐ μετρεῖ. μετρείτω πρότερον· μετρεῖ δὲ καὶ τοὺς Α, Β· ὁ Δ ἄρα τοὺς Α, Β, Γ μετρεῖ· ὁ Δ ἄρα τῶν Α, Β, Γ κοινὸν μέτρον ἐστίν. λέγω δή, ὅτι καὶ μέγιστον. εἰ γὰρ μή ἐστιν ὁ Δ τῶν Α, Β, Γ μέγιστον κοινὸν μέτρον, μετρήσει τις τοὺς Α, Β, Γ ἀριθμοὺς ἀριθμὸς μείζων ὢν τοῦ Δ. μετρείτω, καὶ ἔστω ὁ Ε. ἐπεὶ οὖν ὁ Ε τοὺς Α, Β, Γ μετρεῖ, καὶ τοὺς Α, Β ἄρα μετρήσει· καὶ τὸ τῶν Α, Β ἄρα μέγιστον κοινὸν μέτρον μετρήσει. τὸ δὲ τῶν Α, Β μέγιστον κοινὸν μέτρον ἐστὶν ὁ Δ· ὁ Ε ἄρα τὸν Δ μετρεῖ ὁ μείζων τὸν ἐλάσσονα· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα τοὺς Α, Β, Γ ἀριθμοὺς ἀριθμός τις μετρήσει μείζων ὢν τοῦ Δ· ὁ Δ ἄρα τῶν Α, Β, Γ μέγιστόν ἐστι κοινὸν μέτρον.
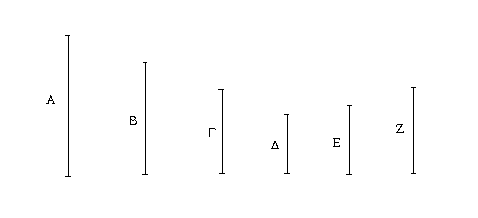
Μὴ μετρείτω δὴ ὁ Δ τὸν Γ· λέγω πρῶτον, ὅτι οἱ Γ, Δ οὔκ εἰσι πρῶτοι πρὸς ἀλλήλους. ἐπεὶ γὰρ οἱ Α, Β, Γ οὔκ εἰσι πρῶτοι πρὸς ἀλλήλους, μετρήσει τις αὐτοὺς ἀριθμός. ὁ δὴ τοὺς Α, Β, Γ μετρῶν καὶ τοὺς Α, Β μετρήσει, καὶ τὸ τῶν Α, Β μέγιστον κοινὸν μέτρον τὸν Δ μετρήσει· μετρεῖ δὲ καὶ τὸν Γ· τοὺς Δ, Γ ἄρα ἀριθμοὺς ἀριθμός τις μετρήσει· οἱ Δ, Γ ἄρα οὔκ εἰσι πρῶτοι πρὸς ἀλλήλους. εἰλήφθω οὖν αὐτῶν τὸ μέγιστον κοινὸν μέτρον ὁ Ε. καὶ ἐπεὶ ὁ Ε τὸν Δ μετρεῖ, ὁ δὲ Δ τοὺς Α, Β μετρεῖ, καὶ ὁ Ε ἄρα τοὺς Α, Β μετρεῖ· μετρεῖ δὲ καὶ τὸν Γ· ὁ Ε ἄρα τοὺς Α, Β, Γ μετρεῖ· ὁ Ε ἄρα τῶν Α, Β, Γ κοινόν ἐστι μέτρον. λέγω δή, ὅτι καὶ μέγιστον. εἰ γὰρ μή ἐστιν ὁ Ε τῶν Α, Β, Γ τὸ μέγιστον κοινὸν μέτρον, μετρήσει τις τοὺς Α, Β, Γ ἀριθμοὺς ἀριθμὸς μείζων ὢν τοῦ Ε. μετρείτω, καὶ ἔστω ὁ Ζ. καὶ ἐπεὶ ὁ Ζ τοὺς Α, Β, Γ μετρεῖ, καὶ τοὺς Α, Β μετρεῖ· καὶ τὸ τῶν Α, Β ἄρα μέγιστον κοινὸν μέτρον μετρήσει. τὸ δὲ τῶν Α, Β μέγιστον κοινὸν μέτρον ἐστὶν ὁ Δ· ὁ Ζ ἄρα τὸν Δ μετρεῖ· μετρεῖ δὲ καὶ τὸν Γ· ὁ Ζ ἄρα τοὺς Δ, Γ μετρεῖ· καὶ τὸ τῶν Δ, Γ ἄρα μέγιστον κοινὸν μέτρον μετρήσει. τὸ δὲ τῶν Δ, Γ μέγιστον κοινὸν μέτρον ἐστὶν ὁ Ε· ὁ Ζ ἄρα τὸν Ε μετρεῖ ὁ μείζων τὸν ἐλάσσονα· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα τοὺς Α, Β, Γ ἀριθμοὺς ἀριθμός τις μετρήσει μείζων ὢν τοῦ Ε· ὁ Ε ἄρα τῶν Α, Β, Γ μέγιστόν ἐστι κοινὸν μέτρον· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ζ΄.
Περιεχόμενα Στοιχείων Εὐκλείδου
Copyright©1999 Dimitrios E. Mourmouras