Στοιχεία Εὐκλείδου ς΄
[Βιβλίον VI]
Αἱ Προτάσεις τῶν Στοιχείων ς΄.
Ἑπομένη Πρότασις
Πρότασις α΄. [1]
Τὰ τρίγωνα καὶ τὰ παραλληλόγραμμα, τὰ ὑπὸ τὸ αὐτὸ ὕψος ὄντα πρὸς ἄλληλά ἐστιν ὡς αἱ βάσεις.
Ἔστω τρίγωνα μὲν τὰ ΑΒΓ, ΑΓΔ, παραλληλόγραμμα δὲ τὰ ΕΓ, ΓΖ ὑπὸ τὸ αὐτὸ ὕψος τὸ ΑΓ· λέγω, ὅτι ἐστὶν ὡς ἡ ΒΓ βάσις πρὸς τὴν ΓΔ βάσιν, οὕτως τὸ ΑΒΓ τρίγωνον πρὸς τὸ ΑΓΔ τρίγωνον, καὶ τὸ ΕΓ παραλληλόγραμμον πρὸς τὸ ΓΖ παραλληλόγραμμον.
Ἐκβεβλήσθω γὰρ ἡ ΒΔ ἐφ' ἑκάτερα τὰ μέρη ἐπὶ τὰ Θ, Λ σημεῖα, καὶ κείσθωσαν τῇ μὲν ΒΓ βάσει ἴσαι [ὁσαιδηποτοῦν] αἱ ΒΗ, ΗΘ, τῇ δὲ ΓΔ βάσει ἴσαι ὁσαιδηποτοῦν αἱ ΔΚ, ΚΛ, καὶ ἐπεζεύχθωσαν αἱ ΑΗ, ΑΘ, ΑΚ, ΑΛ.
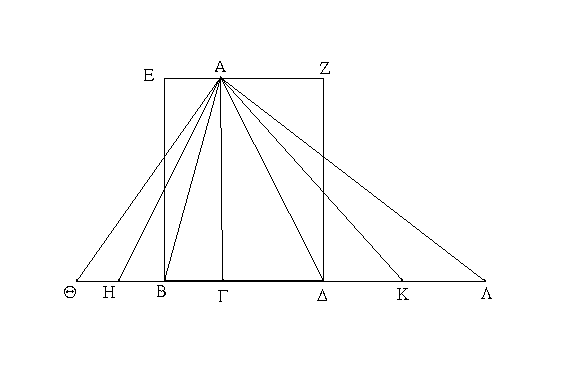
Καὶ ἐπεὶ ἴσαι εἰσὶν αἱ ΓΒ, ΒΗ, ΗΘ ἀλλήλαις, ἴσα ἐστὶ καὶ τὰ ΑΘΗ, ΑΗΒ, ΑΒΓ τρίγωνα ἀλλήλοις. ὁσαπλασίων ἄρα ἐστὶν ἡ ΘΓ βάσις τῆς ΒΓ βάσεως, τοσαυταπλάσιόν ἐστι καὶ τὸ ΑΘΓ τρίγωνον τοῦ ΑΒΓ τριγώνου. διὰ τὰ αὐτὰ δὴ ὁσαπλασίων ἐστὶν ἡ ΛΓ βάσις τῆς ΓΔ βάσεως, τοσαυταπλάσιόν ἐστι καὶ τὸ ΑΛΓ τρίγωνον τοῦ ΑΓΔ τριγώνου· καὶ εἰ ἴση ἐστὶν ἡ ΘΓ βάσις τῇ ΓΛ βάσει, ἴσον ἐστὶ καὶ τὸ ΑΘΓ τρίγωνον τῷ ΑΓΛ τριγώνῳ, καὶ εἰ ὑπερέχει ἡ ΘΓ βάσις τῆς ΓΛ βάσεως, ὑπερέχει καὶ τὸ ΑΘΓ τρίγωνον τοῦ ΑΓΛ τριγώνου, καὶ εἰ ἐλάσσων, ἔλασσον. τεσσάρων δὴ ὄντων μεγεθῶν δύο μὲν βάσεων τῶν ΒΓ, ΓΔ, δύο δὲ τριγώνων τῶν ΑΒΓ, ΑΓΔ εἴληπται ἰσάκις πολλαπλάσια τῆς μὲν ΒΓ βάσεως καὶ τοῦ ΑΒΓ τριγώνου ἥ τε ΘΓ βάσις καὶ τὸ ΑΘΓ τρίγωνον, τῆς δὲ ΓΔ βάσεως καὶ τοῦ ΑΔΓ τριγώνου ἄλλα, ἃ ἔτυχεν, ἰσάκις πολλαπλάσια ἥ τε ΛΓ βάσις καὶ τὸ ΑΛΓ τρίγωνον· καὶ δέδεικται, ὅτι, εἰ ὑπερέχει ἡ ΘΓ βάσις τῆς ΓΛ βάσεως, ὑπερέχει καὶ τὸ ΑΘΓ τρίγωνον τοῦ ΑΛΓ τριγώνου, καὶ εἰ ἴση, ἴσον, καὶ εἰ ἐλάσσων, ἔλασσον· ἔστιν ἄρα ὡς ἡ ΒΓ βάσις πρὸς τὴν ΓΔ βάσιν, οὕτως τὸ ΑΒΓ τρίγωνον πρὸς τὸ ΑΓΔ τρίγωνον.
Καὶ ἐπεὶ τοῦ μὲν ΑΒΓ τριγώνου διπλάσιόν ἐστι τὸ ΕΓ παραλληλόγραμμον, τοῦ δὲ ΑΓΔ τριγώνου διπλάσιόν ἐστι τὸ ΖΓ παραλληλόγραμμον, τὰ δὲ μέρη τοῖς ὡσαύτως πολλαπλασίοις τὸν αὐτὸν ἔχει λόγον, ἔστιν ἄρα ὡς τὸ ΑΒΓ τρίγωνον πρὸς τὸ ΑΓΔ τρίγωνον, οὕτως τὸ ΕΓ παραλληλόγραμμον πρὸς τὸ ΖΓ παραλληλόγραμμον. ἐπεὶ οὖν ἐδείχθη, ὡς μὲν ἡ ΒΓ βάσις πρὸς τὴν ΓΔ, οὕτως τὸ ΑΒΓ τρίγωνον πρὸς τὸ ΑΓΔ τρίγωνον, ὡς δὲ τὸ ΑΒΓ τρίγωνον πρὸς τὸ ΑΓΔ τρίγωνον, οὕτως τὸ ΕΓ παραλληλόγραμμον πρὸς τὸ ΓΖ παραλληλόγραμμον, καὶ ὡς ἄρα ἡ ΒΓ βάσις πρὸς τὴν ΓΔ βάσιν, οὕτως τὸ ΕΓ παραλληλόγραμμον πρὸς τὸ ΖΓ παραλληλόγραμμον.
Τὰ ἄρα τρίγωνα καὶ τὰ παραλληλόγραμμα τὰ ὑπὸ τὸ αὐτὸ ὕψος ὄντα πρὸς ἄλληλά ἐστιν ὡς αἱ βάσεις· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ς΄.
Περιεχόμενα Στοιχείων Εὐκλείδου
Copyright©1999 Dimitrios E. Mourmouras