Στοιχεία Εὐκλείδου α΄
[Βιβλίον I]
Αἱ Προτάσεις τῶν Στοιχείων α΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις β΄. [2]
Πρὸς τῷ δοθέντι σημείῳ τῇ δοθείσῃ εὐθείᾳ ἴσην εὐθεῖαν θέσθαι.
Ἔστω τὸ μὲν δοθὲν σημεῖον τὸ Α, ἡ δὲ δοθεῖσα εὐθεῖα ἡ ΒΓ· δεῖ δὴ πρὸς τῷ Α σημείῳ τῇ δοθείσῃ εὐθείᾳ τῇ ΒΓ ἴσην εὐθεῖαν θέσθαι.
Ἐπεζεύχθω γὰρ ἀπὸ τοῦ Α σημείου ἐπὶ τὸ Β σημεῖον εὐθεῖα ἡ ΑΒ, καὶ συνεστάτω ἐπ' αὐτῆς τρίγωνον ἰσόπλευρον τὸ ΔΑΒ, καὶ ἐκβεβλήσθωσαν ἐπ' εὐθείας ταῖς ΔΑ, ΔΒ εὐθεῖαι αἱ ΑΕ, ΒΖ, καὶ κέντρῳ μὲν τῷ Β διαστήματι δὲ τῷ ΒΓ κύκλος γεγράφθω ὁ ΓΗΘ, καὶ πάλιν κέντρῳ τῷ Δ καὶ διαστήματι τῷ ΔΗ κύκλος γεγράφθω ὁ ΗΚΛ.
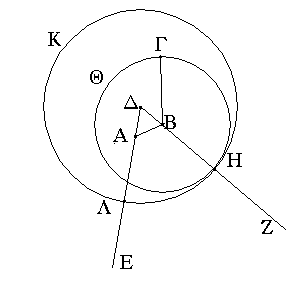
Ἐπεὶ οὖν τὸ Β σημεῖον κέντρον ἐστὶ τοῦ ΓΗΘ κύκλου, ἴση ἐστὶν ἡ ΒΓ τῇ ΒΗ. πάλιν, ἐπεὶ τὸ Δ σημεῖον κέντρον ἐστὶ τοῦ ΚΛΗ κύκλου, ἴση ἐστὶν ἡ ΔΛ τῇ ΔΗ, ὧν ἡ ΔΑ τῇ ΔΒ ἴση ἐστίν. λοιπὴ ἄρα ἡ ΑΛ λοιπῇ τῇ ΒΗ ἐστὶν ἴση. ἐδείχθη δὲ καὶ ἡ ΒΓ τῇ ΒΗ ἴση· ἑκατέρα ἄρα τῶν ΑΛ, ΒΓ τῇ ΒΗ ἐστὶν ἴση. τὰ δὲ τῷ αὐτῷ ἴσα καὶ ἀλλήλοις ἐστὶν ἴσα· καὶ ἡ ΑΛ ἄρα τῇ ΒΓ ἐστὶν ἴση.
Πρὸς ἄρα τῷ δοθέντι σημείῳ τῷ Α τῇ δοθείσῃ εὐθείᾳ τῇ ΒΓ ἴση εὐθεῖα κεῖται ἡ ΑΛ· ὅπερ ἔδει ποιῆσαι.
Μετάφραση Σχόλια Διασυνδέσεις
Θεώρημα β΄ [2]
Σε δεδομένο σημείο να κατασκευασθεί ευθεία ίση με δεδομένη ευθεία.
Έστω ότι το δεδομένο σημείο είναι το σημείο Α, και η δεδομένη ευθεία η ΒΓ , πρέπει να κατασκευαστεί στο σημείο Α ευθεία ίση με την ΒΓ.
Ενώνω το σημείο Α με το σημείο Β και εχω την ευθεία ΑΒ, και σε αυτήν κατασκευάζω το ισόπλευρο τρίγωνο ΔΑΒ (Θεώρ_α΄1) και προεκτείνω τις ευθείες ΔΑ και ΔΒ στις νέες ΑΕ και ΒΖ, και με κέντρο το σημείο Β και διάστημα το ΒΓ γράφω κύκλο τον ΓΗΘ, επίσης με κέντρο το σημείο Δ και διάστημα ΔΗ γράφω τον κύκλο ΗΚΛ.

Επειδή λοιπόν το σημείο Β είναι κέντρο του κύκλου ΓΗΘ, η ΒΓ είναι ίση με την ΒΗ. Επειδή το σημείο Δ είναι κέντρο του κύκλου ΚΛΗ τότε η ΔΛ είναι ίση με την ΔΗ, των οποίων τα μέρη ΔΑ και ΔΒ είναι ίσα. Άρα τα υπόλοιπα ΑΛ και ΒΗ είναι και αυτά ίσα μεταξύ τους (κ.έν.γ΄). Κάθε μία επομένως απ’ τις ΑΛ, ΒΓ είναι ίση με την ΒΗ. Τα προς το αυτό ίσα είναι και μεταξύ τους ίσα (κ.έν.α΄), άρα και η ΑΛ είναι ίση με την ΒΓ.
Άρα από το δεδομένο σημείο το Α κατασκευάστηκε η ευθεία ΑΛ ίση με την δεδομένη ευθεία ΒΓ, όπερ έδει ποιήσαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων α΄.
Περιεχόμενα Στοιχείων Εὐκλείδου
Copyright©1999 Dimitrios E. Mourmouras