Στοιχεία Εὐκλείδου α΄

[Βιβλίον I]

Αἱ Προτάσεις τῶν Στοιχείων α΄.
Ἑπομένη Πρότασις

Πρότασις α΄. [1]

Ἐπὶ τῆς δοθείσης εὐθείας πεπερασμένης τρίγωνον ἰσόπλευρον συστήσασθαι.

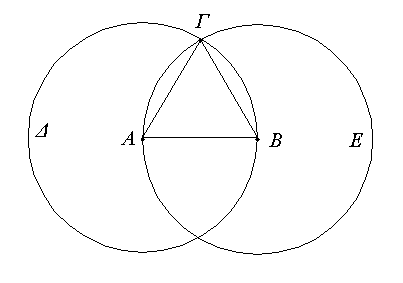
Ἔστω ἡ δοθεῖσα εὐθεῖα πεπερασμένη ἡ ΑΒ. Δεῖ δὴ ἐπὶ τῆς ΑΒ εὐθείας τρίγωνον ἰσόπλευρον συστήσασθαι. Κέντρῳ μὲν τῷ Α διαστήματι δὲ τῷ ΑΒ κύκλος γεγράφθω ὁ ΒΓΔ, καὶ πάλιν κέντρῳ μὲν τῷ Β διαστήματι δὲ τῷ ΒΑ κύκλος γεγράφθω ὁ ΑΓΕ, καὶ ἀπὸ τοῦ Γ σημείου, καθ' ὃ τέμνουσιν ἀλλήλους

οἱ κύκλοι, ἐπὶ τὰ Α, Β σημεῖα ἐπεζεύχθωσαν εὐθεῖαι αἱ ΓΑ, ΓΒ. Καὶ ἐπεὶ τὸ Α σημεῖον κέντρον ἐστὶ τοῦ ΓΔΒ κύκλου, ἴση ἐστὶν ἡ ΑΓ τῇ ΑΒ· πάλιν, ἐπεὶ τὸ Β σημεῖον κέντρον ἐστὶ τοῦ ΓΑΕ κύκλου, ἴση ἐστὶν ἡ ΒΓ τῇ ΒΑ. ἐδείχθη δὲ καὶ ἡ ΓΑ τῇ ΑΒ ἴση· ἑκατέρα ἄρα τῶν ΓΑ, ΓΒ τῇ ΑΒ ἐστὶν ἴση. τὰ δὲ τῷ αὐτῷ ἴσα καὶ ἀλλήλοις ἐστὶν ἴσα· καὶ ἡ ΓΑ ἄρα τῇ ΓΒ ἐστὶν ἴση· αἱ τρεῖς ἄρα αἱ ΓΑ, ΑΒ, ΒΓ ἴσαι ἀλλήλαις εἰσίν. Ἰσόπλευρον ἄρα ἐστὶ τὸ ΑΒΓ τρίγωνον, καὶ συνέσταται ἐπὶ τῆς δοθείσης εὐθείας πεπερασμένης τῆς ΑΒ. [Ἐπὶ τῆς δοθείσης ἄρα εὐθείας πεπερασμένης τρίγωνον ἰσόπλευρον συνέσταται]· ὅπερ ἔδει ποιῆσαι.

Μετάφραση Σχόλια Διασυνδέσεις

Θεώρημα α΄ [1]

Να κατασκευαστεί ισόπλευρο τρίγωνο πάνω σε δεδομένη πεπερασμένη ευθεία.

Έστω η δεδομένη πεπερασμένη ευθεία ΑΒ.

Ζητείτε να κατασκευασθεί πάνω στην ευθεία ΑΒ ισόπλευρο τρίγωνο.

Με κέντρο το σημείο Α και με ακτίνα το διάστημα ΑΒ γράφω τον κύκλο ΒΓΔ, επίσης με κέντρο το σημείο Β και με ακτίνα το διάστημα ΒΑ γράφω τον κύκλο ΑΓΕ, και από το σημείο Γ, στο οποίο τέμνονται μεταξύ τους οι δύο κύκλοι, φέρω τις ευθείες ΓΑ και ΓΒ.

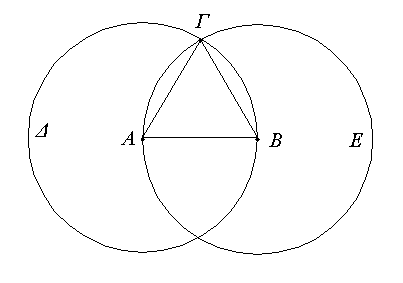
Επειδή το σημείο Α είναι το κέντρο του κύκλου ΓΔΒ, η ΑΓ είναι ίση με την ΑΒ, επίσης,επειδή το σημείο Β είναι το κέντρο του κύκλου ΓΑΕ, η ΒΓ είναι ίση με την ΒΑ. Αποδείχτηκε λοιπόν ότι και η ΓΑ είναι ίση με την ΑΒ, άρα και οι δύο πλευρές οι ΓΑ και ΓΒ είναι ίσες με την ΑΒ. Τα προς το αυτό ίσα είναι και μεταξύ τους ίσα (κ.ἔν.α΄). Άρα η ΓΑ είναι ίση με την ΓΒ, άρα και οι τρεις ευθείες ΓΑ, ΑΒ, ΒΓ είναι μεταξύ τους ίσες.

Άρα το τρίγωνο ΑΒΓ είναι ισόπλευρο και κατασκευάστηκε πάνω στην δεδομένη πεπερασμένη ευθεία ΑΒ.

[Άρα πάνω σε δεδομένη πεπερασμένη ευθεία κατασκευάστηκε ισόπλευρο τρίγωνο], όπερ έδει ποιήσαι.

Ἑπομένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων α΄.
Περιεχόμενα Στοιχείων Εὐκλείδου