Στοιχεία Εὐκλείδου γ΄
[Βιβλίον III]
Αἱ Προτάσεις τῶν Στοιχείων γ΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις κε΄. [25]
Κύκλου τμήματος δοθέντος προσαναγράψαι τὸν κύκλον, οὗπέρ ἐστι τμῆμα.
Ἔστω τὸ δοθὲν τμῆμα κύκλου τὸ ΑΒΓ· δεῖ δὴ τοῦ ΑΒΓ τμήματος προσαναγράψαι τὸν κύκλον, οὗπέρ ἐστι τμῆμα.
Τετμήσθω γὰρ ἡ ΑΓ δίχα κατὰ τὸ Δ, καὶ ἤχθω ἀπὸ τοῦ Δ σημείου τῇ ΑΓ πρὸς ὀρθὰς ἡ ΔΒ, καὶ ἐπεζεύχθω ἡ ΑΒ· ἡ ὑπὸ ΑΒΔ γωνία ἄρα τῆς ὑπὸ ΒΑΔ ἤτοι μείζων ἐστὶν ἢ ἴση ἢ ἐλάττων.
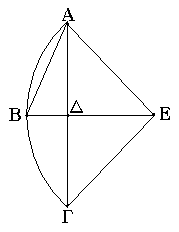
Ἔστω πρότερον μείζων, καὶ συνεστάτω πρὸς τῇ ΒΑ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Α τῇ ὑπὸ ΑΒΔ γωνίᾳ ἴση ἡ ὑπὸ ΒΑΕ, καὶ διήχθω ἡ ΔΒ ἐπὶ τὸ Ε, καὶ ἐπεζεύχθω ἡ ΕΓ. ἐπεὶ οὖν ἴση ἐστὶν ἡ ὑπὸ ΑΒΕ γωνία τῇ ὑπὸ ΒΑΕ, ἴση ἄρα ἐστὶ καὶ ἡ ΕΒ εὐθεῖα τῇ ΕΑ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΔ τῇ ΔΓ, κοινὴ δὲ ἡ ΔΕ, δύο δὴ αἱ ΑΔ, ΔΕ δύο ταῖς ΓΔ, ΔΕ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ· καὶ γωνία ἡ ὑπὸ ΑΔΕ γωνίᾳ τῇ ὑπὸ ΓΔΕ ἐστιν ἴση· ὀρθὴ γὰρ ἑκατέρα· βάσις ἄρα ἡ ΑΕ βάσει τῇ ΓΕ ἐστιν ἴση. ἀλλὰ ἡ ΑΕ τῇ ΒΕ ἐδείχθη ἴση· καὶ ἡ ΒΕ ἄρα τῇ ΓΕ ἐστιν ἴση· αἱ τρεῖς ἄρα αἱ ΑΕ, ΕΒ, ΕΓ ἴσαι ἀλλήλαις εἰσίν· ὁ ἄρα κέντρῳ τῷ Ε διαστήματι δὲ ἑνὶ τῶν ΑΕ, ΕΒ, ΕΓ κύκλος γραφόμενος ἥξει καὶ διὰ τῶν λοιπῶν σημείων καὶ ἔσται προσαναγεγραμμένος. κύκλου ἄρα τμήματος δοθέντος προσαναγέγραπται ὁ κύκλος. καὶ δῆλον, ὡς τὸ ΑΒΓ τμῆμα ἔλαττόν ἐστιν ἡμικυκλίου διὰ τὸ τὸ Ε κέντρον ἐκτὸς αὐτοῦ τυγχάνειν.
Ὁμοίως [δὲ] κἂν ᾖ ἡ ὑπὸ ΑΒΔ γωνία ἴση τῇ ὑπὸ ΒΑΔ, τῆς ΑΔ ἴσης γενομένης ἑκατέρᾳ τῶν ΒΔ, ΔΓ αἱ τρεῖς αἱ ΔΑ, ΔΒ, ΔΓ ἴσαι ἀλλήλαις ἔσονται, καὶ ἔσται τὸ Δ κέντρον τοῦ προσαναπεπληρωμένου κύκλου, καὶ δηλαδὴ ἔσται τὸ ΑΒΓ ἡμικύκλιον.
Ἐὰν δὲ ἡ ὑπὸ ΑΒΔ ἐλάττων ᾖ τῆς ὑπὸ ΒΑΔ, καὶ συστησώμεθα πρὸς τῇ ΒΑ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Α τῇ ὑπὸ ΑΒΔ γωνίᾳ ἴσην, ἐντὸς τοῦ ΑΒΓ τμήματος πεσεῖται τὸ κέντρον ἐπὶ τῆς ΔΒ, καὶ ἔσται δηλαδὴ τὸ ΑΒΓ τμῆμα μεῖζον ἡμικυκλίου.
Κύκλου ἄρα τμήματος δοθέντος προσαναγέγραπται ὁ κύκλος· ὅπερ ἔδει ποιῆσαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων γ΄.
Περιεχόμενα Στοιχείων Εὐκλείδου
Copyright©1999 Dimitrios E. Mourmouras