Στοιχεία Εὐκλείδου ιγ΄
[Βιβλίον XIII]
Αἱ Προτάσεις τῶν Στοιχείων ιγ΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις ια΄. [11]
Ἐὰν εἰς κύκλον ῥητὴν ἔχοντα τὴν διάμετρον πεντάγωνον ἰσόπλευρον ἐγγραφῇ, ἡ τοῦ πενταγώνου πλευρὰ ἄλογός ἐστιν ἡ καλουμένη ἐλάσσων.
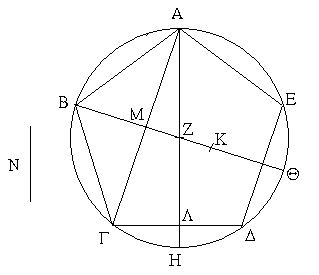
Εἰς γὰρ κύκλον τὸν ΑΒΓΔΕ ῥητὴν ἔχοντα τὴν διάμετρον πεντάγωνον ἰσόπλευρον ἐγγεγράφθω τὸ ΑΒΓΔΕ· λέγω, ὅτι ἡ τοῦ [ΑΒΓΔΕ] πενταγώνου πλευρὰ ἄλογός ἐστιν ἡ καλουμένη ἐλάσσων.
Εἰλήφθω γὰρ τὸ κέντρον τοῦ κύκλου τὸ Ζ σημεῖον, καὶ ἐπεζεύχθωσαν αἱ ΑΖ, ΖΒ καὶ διήχθωσαν ἐπὶ τὰ Η, Θ σημεῖα, καὶ ἐπεζεύχθω ἡ ΑΓ, καὶ κείσθω τῆς ΑΖ τέταρτον μέρος ἡ ΖΚ. ῥητὴ δὲ ἡ ΑΖ· ῥητὴ ἄρα καὶ ἡ ΖΚ. ἔστι δὲ καὶ ἡ ΒΖ ῥητή· ὅλη ἄρα ἡ ΒΚ ῥητή ἐστιν. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΓΗ περιφέρεια τῇ ΑΔΗ περιφερείᾳ, ὧν ἡ ΑΒΓ τῇ ΑΕΔ ἐστιν ἴση, λοιπὴ ἄρα ἡ ΓΗ λοιπῇ τῇ ΗΔ ἐστιν ἴση. καὶ ἐὰν ἐπιζεύξωμεν τὴν ΑΔ, συνάγονται ὀρθαὶ αἱ πρὸς τῷ Λ γωνίαι, καὶ διπλῆ ἡ ΓΔ τῆς ΓΛ. διὰ τὰ αὐτὰ δὴ καὶ αἱ πρὸς τῷ Μ ὀρθαί εἰσιν, καὶ διπλῆ ἡ ΑΓ τῆς ΓΜ. ἐπεὶ οὖν ἴση ἐστὶν ἡ ὑπὸ ΑΛΓ γωνία τῇ ὑπὸ ΑΜΖ, κοινὴ δὲ τῶν δύο τριγώνων τοῦ τε ΑΓΛ καὶ τοῦ ΑΜΖ ἡ ὑπὸ ΛΑΓ, λοιπὴ ἄρα ἡ ὑπὸ ΑΓΛ λοιπῇ τῇ ὑπὸ ΜΖΑ ἐστιν ἴση· ἰσογώνιον ἄρα ἐστὶ τὸ ΑΓΛ τρίγωνον τῷ ΑΜΖ τριγώνῳ· ἀνάλογον ἄρα ἐστὶν ὡς ἡ ΛΓ πρὸς ΓΑ, οὕτως ἡ ΜΖ πρὸς ΖΑ· καὶ τῶν ἡγουμένων τὰ διπλάσια· ὡς ἄρα ἡ τῆς ΛΓ διπλῆ πρὸς τὴν ΓΑ, οὕτως ἡ τῆς ΜΖ διπλῆ πρὸς τὴν ΖΑ. ὡς δὲ ἡ τῆς ΜΖ διπλῆ πρὸς τὴν ΖΑ, οὕτως ἡ ΜΖ πρὸς τὴν ἡμίσειαν τῆς ΖΑ· καὶ ὡς ἄρα ἡ τῆς ΛΓ διπλῆ πρὸς τὴν ΓΑ, οὕτως ἡ ΜΖ πρὸς τὴν ἡμίσειαν τῆς ΖΑ. καὶ τῶν ἑπομένων τὰ ἡμίσεα· ὡς ἄρα ἡ τῆς ΛΓ διπλῆ πρὸς τὴν ἡμίσειαν τῆς ΓΑ, οὕτως ἡ ΜΖ πρὸς τὸ τέταρτον τῆς ΖΑ.
καί ἐστι τῆς μὲν ΛΓ διπλῆ ἡ ΔΓ, τῆς δὲ ΓΑ ἡμίσεια ἡ ΓΜ, τῆς δὲ ΖΑ τέταρτον μέρος ἡ ΖΚ· ἔστιν ἄρα ὡς ἡ ΔΓ πρὸς τὴν ΓΜ, οὕτως ἡ ΜΖ πρὸς τὴν ΖΚ. συνθέντι καὶ ὡς συναμφότερος ἡ ΔΓΜ πρὸς τὴν ΓΜ, οὕτως ἡ ΜΚ πρὸς ΚΖ· καὶ ὡς ἄρα τὸ ἀπὸ συναμφοτέρου τῆς ΔΓΜ πρὸς τὸ ἀπὸ ΓΜ, οὕτως τὸ ἀπὸ ΜΚ πρὸς τὸ ἀπὸ ΚΖ. καὶ ἐπεὶ τῆς ὑπὸ δύο πλευρὰς τοῦ πενταγώνου ὑποτεινούσης, οἷον τῆς ΑΓ, ἄκρον καὶ μέσον λόγον τεμνομένης τὸ μεῖζον τμῆμα ἴσον ἐστὶ τῇ τοῦ πενταγώνου πλευρᾷ, τουτέστι τῇ ΔΓ, τὸ δὲ μεῖζον τμῆμα προσλαβὸν τὴν ἡμίσειαν τῆς ὅλης πενταπλάσιον δύναται τοῦ ἀπὸ τῆς ἡμισείας τῆς ὅλης, καί ἐστιν ὅλης τῆς ΑΓ ἡμίσεια ἡ ΓΜ, τὸ ἄρα ἀπὸ τῆς ΔΓΜ ὡς μιᾶς πενταπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΓΜ. ὡς δὲ τὸ ἀπὸ τῆς ΔΓΜ ὡς μιᾶς πρὸς τὸ ἀπὸ τῆς ΓΜ, οὕτως ἐδείχθη τὸ ἀπὸ τῆς ΜΚ πρὸς τὸ ἀπὸ τῆς ΚΖ· πενταπλάσιον ἄρα τὸ ἀπὸ τῆς ΜΚ τοῦ ἀπὸ τῆς ΚΖ. ῥητὸν δὲ τὸ ἀπὸ τῆς ΚΖ· ῥητὴ γὰρ ἡ διάμετρος· ῥητὸν ἄρα καὶ τὸ ἀπὸ τῆς ΜΚ· ῥητὴ ἄρα ἐστὶν ἡ ΜΚ [δυνάμει μόνον]. καὶ ἐπεὶ τετραπλασία ἐστὶν ἡ ΒΖ τῆς ΖΚ, πενταπλασία ἄρα ἐστὶν ἡ ΒΚ τῆς ΚΖ· εἰκοσιπενταπλάσιον ἄρα τὸ ἀπὸ τῆς ΒΚ τοῦ ἀπὸ τῆς ΚΖ. πενταπλάσιον δὲ τὸ ἀπὸ τῆς ΜΚ τοῦ ἀπὸ τῆς ΚΖ· πενταπλάσιον ἄρα τὸ ἀπὸ τῆς ΒΚ τοῦ ἀπὸ τῆς ΚΜ· τὸ ἄρα ἀπὸ τῆς ΒΚ πρὸς τὸ ἀπὸ ΚΜ λόγον οὐκ ἔχει, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ἀσύμμετρος ἄρα ἐστὶν ἡ ΒΚ τῇ ΚΜ μήκει. καί ἐστι ῥητὴ ἑκατέρα αὐτῶν. αἱ ΒΚ, ΚΜ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι. ἐὰν δὲ ἀπὸ ῥητῆς ῥητὴ ἀφαιρεθῇ δυνάμει μόνον σύμμετρος οὖσα τῇ ὅλῃ, ἡ λοιπὴ ἄλογός ἐστιν ἀποτομή· ἀποτομὴ ἄρα ἐστὶν ἡ ΜΒ, προσαρμόζουσα δὲ αὐτῇ ἡ ΜΚ. λέγω δή, ὅτι καὶ τετάρτη. ᾧ δὴ μεῖζόν ἐστι τὸ ἀπὸ τῆς ΒΚ τοῦ ἀπὸ τῆς ΚΜ, ἐκείνῳ ἴσον ἔστω τὸ ἀπὸ τῆς Ν· ἡ ΒΚ ἄρα τῆς ΚΜ μεῖζον δύναται τῇ Ν. καὶ ἐπεὶ σύμμετρός ἐστιν ἡ ΚΖ τῇ ΖΒ, καὶ συνθέντι σύμμετρός ἐστιν ἡ ΚΒ τῇ ΖΒ. ἀλλὰ ἡ ΒΖ τῇ ΒΘ σύμμετρός ἐστιν· καὶ ἡ ΒΚ ἄρα τῇ ΒΘ σύμμετρός ἐστιν. καὶ ἐπεὶ πενταπλάσιόν ἐστι τὸ ἀπὸ τῆς ΒΚ τοῦ ἀπὸ τῆς ΚΜ, τὸ ἄρα ἀπὸ τῆς ΒΚ πρὸς τὸ ἀπὸ τῆς ΚΜ λόγον ἔχει, ὃν ε πρὸς ἕν.ἀναστρέψαντι ἄρα τὸ ἀπὸ τῆς ΒΚ πρὸςυὸ ἀπὸ τῆς Ν λόγον ἔχει, ὅν ε πρὸς δ. οὐχ ὃν τετράγωνος πρὸς τετράγωνον· ἀσύμετρος ἄρα ἐστὶν ἡ ΒΚ τῇ Ν· ἡ ΒΚ ἄρα τῆς ΚΜ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ. ἐπεὶ οὖν ὅλη ἡ ΒΚ τῆς προσαρμοζούσης τῆς ΚΜ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ, καὶ ὅλη ἡ ΒΚ σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ τῇ ΒΘ, ἀποτομὴ ἄρα τετάρτη ἐστὶν ἡ ΜΒ. τὸ δὲ ὑπὸ ῥητῆς καὶ ἀποτομῆς τετάρτης περιεχόμενον ὀρθογώνιον ἄλογόν ἐστιν, καὶ ἡ δυναμένη αὐτὸ ἄλογός ἐστιν, καλεῖται δὲ ἐλάττων. δύναται δὲ τὸ ὑπὸ τῶν ΘΒΜ ἡ ΑΒ διὰ τὸ ἐπιζευγνυμένης τῆς ΑΘ ἰσογώνιον γίνεσθαι τὸ ΑΒΘ τρίγωνον τῷ ΑΒΜ τριγώνῳ καὶ εἶναι ὡς τὴν ΘΒ πρὸς τὴν ΒΑ, οὕτως τὴν ΑΒ πρὸς τὴν ΒΜ.
Ἡ ἄρα ΑΒ τοῦ πενταγώνου πλευρὰ ἄλογός ἐστιν ἡ καλουμένη ἐλάττων· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ιγ΄.
Περιεχόμενα Στοιχείων Εὐκλείδου
Copyright©1999 Dimitrios E. Mourmouras