Στοιχεία Εὐκλείδου ιγ΄
[Βιβλίον XIII]
Αἱ Προτάσεις τῶν Στοιχείων ιγ΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις θ΄. [9]
9Ἐὰν ἡ τοῦ ἑξαγώνου πλευρὰ καὶ ἡ τοῦ δεκαγώνου τῶν εἰς τὸν αὐτὸν κύκλον ἐγγραφομένων συντεθῶσιν, ἡ ὅλη εὐθεῖα ἄκρον καὶ μέσον λόγον τέτμηται, καὶ τὸ μεῖζον αὐτῆς τμῆμά ἐστιν ἡ τοῦ ἑξαγώνου πλευρά.
Ἔστω κύκλος ὁ ΑΒΓ, καὶ τῶν εἰς τὸν ΑΒΓ κύκλον ἐγγραφομένων σχημάτων, δεκαγώνου μὲν ἔστω πλευρὰ ἡ ΒΓ, ἑξαγώνου δὲ ἡ ΓΔ, καὶ ἔστωσαν ἐπ' εὐθείας· λέγω, ὅτι ἡ ὅλη εὐθεῖα ἡ ΒΔ ἄκρον καὶ μέσον λόγον τέτμηται, καὶ τὸ μεῖζον αὐτῆς τμῆμά ἐστιν ἡ ΓΔ.
Εἰλήφθω γὰρ τὸ κέντρον τοῦ κύκλου τὸ Ε σημεῖον, καὶ ἐπεζεύχθωσαν αἱ ΕΒ, ΕΓ, ΕΔ, καὶ διήχθω ἡ ΒΕ ἐπὶ τὸ Α. ἐπεὶ δεκαγώνου ἰσοπλεύρου πλευρά ἐστιν ἡ ΒΓ, πενταπλασίων ἄρα ἡ ΑΓΒ περιφέρεια τῆς ΒΓ περιφερείας· τετραπλασίων ἄρα ἡ ΑΓ περιφέρεια τῆς ΓΒ. ὡς δὲ ἡ ΑΓ περιφέρεια πρὸς τὴν ΓΒ, οὕτως ἡ ὑπὸ ΑΕΓ γωνία πρὸς τὴν ὑπὸ ΓΕΒ· τετραπλασίων ἄρα ἡ ὑπὸ ΑΕΓ τῆς ὑπὸ ΓΕΒ.
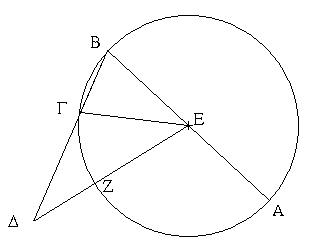
καὶ ἐπεὶ ἴση ἡ ὑπὸ ΕΒΓ γωνία τῇ ὑπὸ ΕΓΒ, ἡ ἄρα ὑπὸ ΑΕΓ γωνία διπλασία ἐστὶ τῆς ὑπὸ ΕΓΒ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΕΓ εὐθεῖα τῇ ΓΔ· ἑκατέρα γὰρ αὐτῶν ἴση ἐστὶ τῇ τοῦ ἑξαγώνου πλευρᾷ τοῦ εἰς τὸν ΑΒΓ κύκλον [ἐγγραφομένου]· ἴση ἐστὶ καὶ ἡ ὑπὸ ΓΕΔ γωνία τῇ ὑπὸ ΓΔΕ γωνίᾳ· διπλασία ἄρα ἡ ὑπὸ ΕΓΒ γωνία τῆς ὑπὸ ΕΔΓ. ἀλλὰ τῆς ὑπὸ ΕΓΒ διπλασία ἐδείχθη ἡ ὑπὸ ΑΕΓ· τετραπλασία ἄρα ἡ ὑπὸ ΑΕΓ τῆς ὑπὸ ΕΔΓ. ἐδείχθη δὲ καὶ τῆς ὑπὸ ΒΕΓ τετραπλασία ἡ ὑπὸ ΑΕΓ· ἴση ἄρα ἡ ὑπὸ ΕΔΓ τῇ ὑπὸ ΒΕΓ. κοινὴ δὲ τῶν δύο τριγώνων, τοῦ τε ΒΕΓ καὶ τοῦ ΒΕΔ, ἡ ὑπὸ ΕΒΔ γωνία· καὶ λοιπὴ ἄρα ἡ ὑπὸ ΒΕΔ τῇ ὑπὸ ΕΓΒ ἐστιν ἴση· ἰσογώνιον ἄρα ἐστὶ τὸ ΕΒΔ τρίγωνον τῷ ΕΒΓ τριγώνῳ. ἀνάλογον ἄρα ἐστὶν ὡς ἡ ΔΒ πρὸς τὴν ΒΕ, οὕτως ἡ ΕΒ πρὸς τὴν ΒΓ. ἴση δὲ ἡ ΕΒ τῇ ΓΔ. ἔστιν ἄρα ὡς ἡ ΒΔ πρὸς τὴν ΔΓ, οὕτως ἡ ΔΓ πρὸς τὴν ΓΒ. μείζων δὲ ἡ ΒΔ τῆς ΔΓ· μείζων ἄρα καὶ ἡ ΔΓ τῆς ΓΒ. ἡ ΒΔ ἄρα εὐθεῖα ἄκρον καὶ μέσον λόγον τέτμηται [κατὰ τὸ Γ], καὶ τὸ μεῖζον τμῆμα αὐτῆς ἐστιν ἡ ΔΓ· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ιγ΄.
Περιεχόμενα Στοιχείων Εὐκλείδου
Copyright©1999 Dimitrios E. Mourmouras