Στοιχεία Εὐκλείδου ια΄
[Βιβλίον XI]
Αἱ Προτάσεις τῶν Στοιχείων ια΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις ια΄. [11]
Ἀπὸ τοῦ δοθέντος σημείου μετεώρου ἐπὶ τὸ δοθὲν ἐπίπεδον κάθετον εὐθεῖαν γραμμὴν ἀγαγεῖν.
Ἔστω τὸ μὲν δοθὲν σημεῖον μετέωρον τὸ Α, τὸ δὲ δοθὲν ἐπίπεδον τὸ ὑποκείμενον· δεῖ δὴ ἀπὸ τοῦ Α σημείου ἐπὶ τὸ ὑποκείμενον ἐπίπεδον κάθετον εὐθεῖαν γραμμὴν ἀγαγεῖν.
Διήχθω γάρ τις ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ εὐθεῖα, ὡς ἔτυχεν, ἡ ΒΓ, καὶ ἤχθω ἀπὸ τοῦ Α σημείου ἐπὶ τὴν ΒΓ κάθετος ἡ ΑΔ. εἰ μὲν οὖν ἡ ΑΔ κάθετός ἐστι καὶ ἐπὶ τὸ ὑποκείμενον ἐπίπεδον, γεγονὸς ἂν εἴη τὸ ἐπιταχθέν. εἰ δὲ οὔ, ἤχθω ἀπὸ τοῦ Δ σημείου τῇ ΒΓ ἐν τῷ ὑποκειμένῳ ἐπιπέδῳ πρὸς ὀρθὰς ἡ ΔΕ, καὶ ἤχθω ἀπὸ τοῦ Α ἐπὶ τὴν ΔΕ κάθετος ἡ ΑΖ, καὶ διὰ τοῦ Ζ σημείου τῇ ΒΓ παράλληλος ἤχθω ἡ ΗΘ.
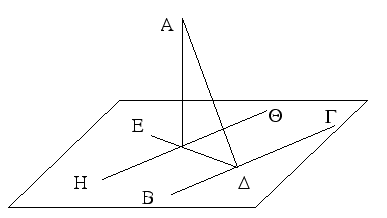
Καὶ ἐπεὶ ἡ ΒΓ ἑκατέρᾳ τῶν ΔΑ, ΔΕ πρὸς ὀρθάς ἐστιν, ἡ ΒΓ ἄρα καὶ τῷ διὰ τῶν ΕΔΑ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν. καί ἐστιν αὐτῇ παράλληλος ἡ ΗΘ· ἐὰν δὲ ὦσι δύο εὐθεῖαι παράλληλοι, ἡ δὲ μία αὐτῶν ἐπιπέδῳ τινὶ πρὸς ὀρθὰς ᾖ, καὶ ἡ λοιπὴ τῷ αὐτῷ ἐπιπέδῳ πρὸς ὀρθὰς ἔσται· καὶ ἡ ΗΘ ἄρα τῷ διὰ τῶν ΕΔ, ΔΑ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν. καὶ πρὸς πάσας ἄρα τὰς ἁπτομένας αὐτῆς εὐθείας καὶ οὔσας ἐν τῷ διὰ τῶν ΕΔ, ΔΑ ἐπιπέδῳ ὀρθή ἐστιν ἡ ΗΘ. ἅπτεται δὲ αὐτῆς ἡ ΑΖ οὖσα ἐν τῷ διὰ τῶν ΕΔ, ΔΑ ἐπιπέδῳ· ἡ ΗΘ ἄρα ὀρθή ἐστι πρὸς τὴν ΖΑ· ὥστε καὶ ἡ ΖΑ ὀρθή ἐστι πρὸς τὴν ΘΗ. ἔστι δὲ ἡ ΑΖ καὶ πρὸς τὴν ΔΕ ὀρθή· ἡ ΑΖ ἄρα πρὸς ἑκατέραν τῶν ΗΘ, ΔΕ ὀρθή ἐστιν. ἐὰν δὲ εὐθεῖα δυσὶν εὐθείαις τεμνούσαις ἀλλήλας ἐπὶ τῆς τομῆς πρὸς ὀρθὰς ἐπισταθῇ, καὶ τῷ δι' αὐτῶν ἐπιπέδῳ πρὸς ὀρθὰς ἔσται· ἡ ΖΑ ἄρα τῷ διὰ τῶν ΕΔ, ΗΘ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν. τὸ δὲ διὰ τῶν ΕΔ, ΗΘ ἐπίπεδόν ἐστι τὸ ὑποκείμενον· ἡ ΑΖ ἄρα τῷ ὑποκειμένῳ ἐπιπέδῳ πρὸς ὀρθάς ἐστιν.
Ἀπὸ τοῦ ἄρα δοθέντος σημείου μετεώρου τοῦ Α ἐπὶ τὸ ὑποκείμενον ἐπίπεδον κάθετος εὐθεῖα γραμμὴ ἦκται ἡ ΑΖ· ὅπερ ἔδει ποιῆσαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ια΄.
Περιεχόμενα Στοιχείων Εὐκλείδου
Copyright©1999 Dimitrios E. Mourmouras