Στοιχεία Εὐκλείδου ς΄

[Βιβλίον VI]

Αἱ Προτάσεις τῶν Στοιχείων ς΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις

Πρότασις δ΄. [4]

Τῶν ἰσογωνίων τριγώνων ἀνάλογόν εἰσιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας καὶ ὁμόλογοι αἱ ὑπὸ τὰς ἴσας γωνίας ὑποτείνουσαι.

Ἔστω ἰσογώνια τρίγωνα τὰ ΑΒΓ, ΔΓΕ ἴσην ἔχοντα τὴν μὲν ὑπὸ ΑΒΓ γωνίαν τῇ ὑπὸ ΔΓΕ, τὴν δὲ ὑπὸ ΒΑΓ τῇ ὑπὸ ΓΔΕ καὶ ἔτι τὴν ὑπὸ ΑΓΒ τῇ ὑπὸ ΓΕΔ· λέγω, ὅτι τῶν ΑΒΓ, ΔΓΕ τριγώνων ἀνάλογόν εἰσιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας καὶ ὁμόλογοι αἱ ὑπὸ τὰς ἴσας γωνίας ὑποτείνουσαι.

Κείσθω γὰρ ἐπ' εὐθείας ἡ ΒΓ τῇ ΓΕ. καὶ ἐπεὶ αἱ ὑπὸ ΑΒΓ, ΑΓΒ γωνίαι δύο ὀρθῶν ἐλάττονές εἰσιν, ἴση δὲ ἡ ὑπὸ ΑΓΒ τῇ ὑπὸ ΔΕΓ, αἱ ἄρα ὑπὸ ΑΒΓ, ΔΕΓ δύο ὀρθῶν ἐλάττονές εἰσιν· αἱ ΒΑ, ΕΔ ἄρα ἐκβαλλόμεναι συμπεσοῦνται. ἐκβεβλήσθωσαν καὶ συμπιπτέτωσαν κατὰ τὸ Ζ.

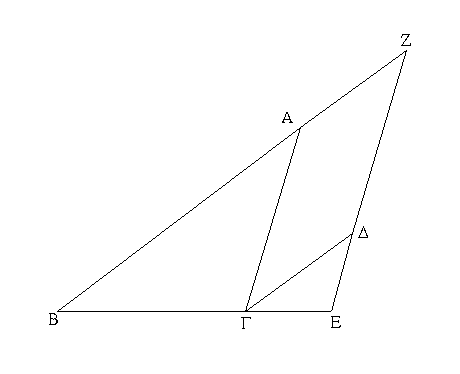
Καὶ ἐπεὶ ἴση ἐστὶν ἡ ὑπὸ ΔΓΕ γωνία τῇ ὑπὸ ΑΒΓ, παράλληλός ἐστιν ἡ ΒΖ τῇ ΓΔ. πάλιν, ἐπεὶ ἴση ἐστὶν ἡ ὑπὸ ΑΓΒ τῇ ὑπὸ ΔΕΓ, παράλληλός ἐστιν ἡ ΑΓ τῇ ΖΕ. παραλληλόγραμμον ἄρα ἐστὶ τὸ ΖΑΓΔ· ἴση ἄρα ἡ μὲν ΖΑ τῇ ΔΓ, ἡ δὲ ΑΓ τῇ ΖΔ. καὶ ἐπεὶ τριγώνου τοῦ ΖΒΕ παρὰ μίαν τὴν ΖΕ ἦκται ἡ ΑΓ, ἔστιν ἄρα ὡς ἡ ΒΑ πρὸς τὴν ΑΖ, οὕτως ἡ ΒΓ πρὸς τὴν ΓΕ. ἴση δὲ ἡ ΑΖ τῇ ΓΔ· ὡς ἄρα ἡ ΒΑ πρὸς τὴν ΓΔ, οὕτως ἡ ΒΓ πρὸς τὴν ΓΕ, καὶ ἐναλλὰξ ὡς ἡ ΑΒ πρὸς τὴν ΒΓ, οὕτως ἡ ΔΓ πρὸς τὴν ΓΕ. πάλιν, ἐπεὶ παράλληλός ἐστιν ἡ ΓΔ τῇ ΒΖ, ἔστιν ἄρα ὡς ἡ ΒΓ πρὸς τὴν ΓΕ, οὕτως ἡ ΖΔ πρὸς τὴν ΔΕ. ἴση δὲ ἡ ΖΔ τῇ ΑΓ· ὡς ἄρα ἡ ΒΓ πρὸς τὴν ΓΕ, οὕτως ἡ ΑΓ πρὸς τὴν ΔΕ, καὶ ἐναλλὰξ ὡς ἡ ΒΓ πρὸς τὴν ΓΑ, οὕτως ἡ ΓΕ πρὸς τὴν ΕΔ. ἐπεὶ οὖν ἐδείχθη ὡς μὲν ἡ ΑΒ πρὸς τὴν ΒΓ, οὕτως ἡ ΔΓ πρὸς τὴν ΓΕ, ὡς δὲ ἡ ΒΓ πρὸς τὴν ΓΑ, οὕτως ἡ ΓΕ πρὸς τὴν ΕΔ, δι' ἴσου ἄρα ὡς ἡ ΒΑ πρὸς τὴν ΑΓ, οὕτως ἡ ΓΔ πρὸς τὴν ΔΕ.

Τῶν ἄρα ἰσογωνίων τριγώνων ἀνάλογόν εἰσιν αἱ πλευραὶ αἱ περὶ τὰς ἴσας γωνίας καὶ ὁμόλογοι αἱ ὑπὸ τὰς ἴσας γωνίας ὑποτείνουσαι· ὅπερ ἔδει δεῖξαι.

Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ς΄.
Περιεχόμενα Στοιχείων Εὐκλείδου