Στοιχεία Εὐκλείδου α΄
[Βιβλίον I]
Αἱ Προτάσεις τῶν Στοιχείων α΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις ιε΄. [15]
Ἐὰν δύο εὐθεῖαι τέμνωσιν ἀλλήλας, τὰς κατὰ κορυφὴν γωνίας ἴσας ἀλλήλαις ποιοῦσιν.
Δύο γὰρ εὐθεῖαι αἱ ΑΒ, ΓΔ τεμνέτωσαν ἀλλήλας κατὰ τὸ Ε σημεῖον· λέγω, ὅτι ἴση ἐστὶν ἡ μὲν ὑπὸ ΑΕΓ γωνία τῇ ὑπὸ ΔΕΒ, ἡ δὲ ὑπὸ ΓΕΒ τῇ ὑπὸ ΑΕΔ.
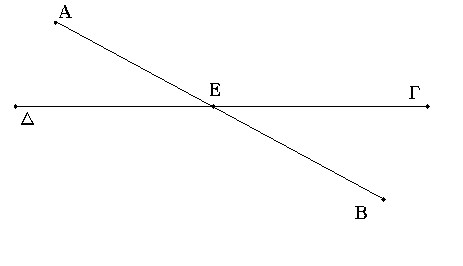
Ἐπεὶ γὰρ εὐθεῖα ἡ ΑΕ ἐπ' εὐθεῖαν τὴν ΓΔ ἐφέστηκε γωνίας ποιοῦσα τὰς ὑπὸ ΓΕΑ, ΑΕΔ, αἱ ἄρα ὑπὸ ΓΕΑ, ΑΕΔ γωνίαι δυσὶν ὀρθαῖς ἴσαι εἰσίν. πάλιν, ἐπεὶ εὐθεῖα ἡ ΔΕ ἐπ' εὐθεῖαν τὴν ΑΒ ἐφέστηκε γωνίας ποιοῦσα τὰς ὑπὸ ΑΕΔ, ΔΕΒ, αἱ ἄρα ὑπὸ ΑΕΔ, ΔΕΒ γωνίαι δυσὶν ὀρθαῖς ἴσαι εἰσίν. ἐδείχθησαν δὲ καὶ αἱ ὑπὸ ΓΕΑ, ΑΕΔ δυσὶν ὀρθαῖς ἴσαι· αἱ ἄρα ὑπὸ ΓΕΑ, ΑΕΔ ταῖς ὑπὸ ΑΕΔ, ΔΕΒ ἴσαι εἰσίν. κοινὴ ἀφῃρήσθω ἡ ὑπὸ ΑΕΔ· λοιπὴ ἄρα ἡ ὑπὸ ΓΕΑ λοιπῇ τῇ ὑπὸ ΒΕΔ ἴση ἐστίν· ὁμοίως δὴ δειχθήσεται, ὅτι καὶ αἱ ὑπὸ ΓΕΒ, ΔΕΑ ἴσαι εἰσίν.
Ἐὰν ἄρα δύο εὐθεῖαι τέμνωσιν ἀλλήλας, τὰς κατὰ κορυφὴν γωνίας ἴσας ἀλλήλαις ποιοῦσιν· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων α΄.
Περιεχόμενα Στοιχείων Εὐκλείδου
Copyright©1999 Dimitrios E. Mourmouras