Στοιχεία Εὐκλείδου ιβ΄
[Βιβλίον XII]
Αἱ Προτάσεις τῶν Στοιχείων ιβ΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις ιζ΄. [17]
Δύο σφαιρῶν περὶ τὸ αὐτὸ κέντρον οὐσῶν εἰς τὴν μείζονα σφαῖραν στερεὸν πολύεδρον ἐγγράψαι μὴ ψαῦον τῆς ἐλάσσονος σφαίρας κατὰ τὴν ἐπιφάνειαν.
Νενοήσθωσαν δύο σφαῖραι περὶ τὸ αὐτὸ κέντρον τὸ Α· δεῖ δὴ εἰς τὴν μείζονα σφαῖραν στερεὸν πολύεδρον ἐγγράψαι μὴ ψαῦον τῆς ἐλάσσονος σφαίρας κατὰ τὴν ἐπιφάνειαν.
Τετμήσθωσαν αἱ σφαῖραι ἐπιπέδῳ τινὶ διὰ τοῦ κέντρου· ἔσονται δὴ αἱ τομαὶ κύκλοι, ἐπειδήπερ μενούσης τῆς διαμέτρου καὶ περιφερομένου τοῦ ἡμικυκλίου ἐγίγνετο ἡ σφαῖρα· ὥστε καὶ καθ' οἵας ἂν θέσεως ἐπινοήσωμεν τὸ ἡμικύκλιον, τὸ δι' αὐτοῦ ἐκβαλλόμενον ἐπίπεδον ποιήσει ἐπὶ τῆς ἐπιφανείας τῆς σφαίρας κύκλον. καὶ φανερόν, ὅτι καὶ μέγιστον, ἐπειδήπερ ἡ διάμετρος τῆς σφαίρας, ἥτις ἐστὶ καὶ τοῦ ἡμικυκλίου διάμετρος δηλαδὴ καὶ τοῦ κύκλου, μείζων ἐστὶ πασῶν τῶν εἰς τὸν κύκλον ἢ τὴν σφαῖραν διαγομένων [εὐθειῶν]. ἔστω οὖν ἐν μὲν τῇ μείζονι σφαίρᾳ κύκλος ὁ ΒΓΔΕ, ἐν δὲ τῇ ἐλάσσονι σφαίρᾳ κύκλος ὁ ΖΗΘ, καὶ ἤχθωσαν αὐτῶν δύο διάμετροι πρὸς ὀρθὰς ἀλλήλαις αἱ ΒΔ, ΓΕ, καὶ δύο κύκλων περὶ τὸ αὐτὸ κέντρον ὄντων τῶν ΒΓΔΕ, ΖΗΘ εἰς τὸν μείζονα κύκλον τὸν ΒΓΔΕ πολύγωνον ἰσόπλευρον καὶ ἀρτιόπλευρον ἐγγεγράφθω μὴ ψαῦον τοῦ ἐλάσσονος κύκλου τοῦ ΖΗΘ, οὗ πλευραὶ ἔστωσαν ἐν τῷ ΒΕ τεταρτημορίῳ αἱ ΒΚ, ΚΛ, ΛΜ, ΜΕ, καὶ ἐπιζευχθεῖσα ἡ ΚΑ διήχθω ἐπὶ τὸ Ν, καὶ ἀνεστάτω ἀπὸ τοῦ Α σημείου τῷ τοῦ ΒΓΔΕ κύκλου ἐπιπέδῳ πρὸς ὀρθὰς ἡ ΑΞ καὶ συμβαλλέτω τῇ ἐπιφανείᾳ τῆς σφαίρας κατὰ τὸ Ξ, καὶ διὰ τῆς ΑΞ καὶ ἑκατέρας τῶν ΒΔ, ΚΝ ἐπίπεδα ἐκβεβλήσθω· ποιήσουσι δὴ διὰ τὰ εἰρημένα ἐπὶ τῆς ἐπιφανείας τῆς σφαίρας μεγίστους κύκλους. ποιείτωσαν, ὧν ἡμικύκλια ἔστω ἐπὶ τῶν ΒΔ, ΚΝ διαμέτρων τὰ ΒΞΔ, ΚΞΝ. καὶ ἐπεὶ ἡ ΞΑ ὀρθή ἐστι πρὸς τὸ τοῦ ΒΓΔΕ κύκλου ἐπίπεδον, καὶ πάντα ἄρα τὰ διὰ τῆς ΞΑ ἐπίπεδά ἐστιν ὀρθὰ πρὸς τὸ τοῦ ΒΓΔΕ κύκλου ἐπίπεδον·
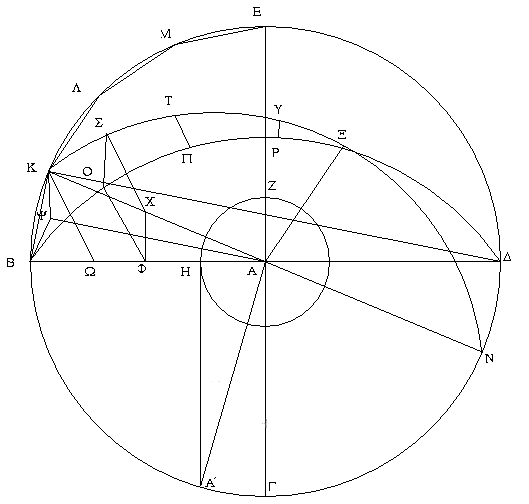
ὥστε καὶ τὰ ΒΞΔ, ΚΞΝ ἡμικύκλια ὀρθά ἐστι πρὸς τὸ τοῦ ΒΓΔΕ κύκλου ἐπίπεδον. καὶ ἐπεὶ ἴσα ἐστὶ τὰ ΒΕΔ, ΒΞΔ, ΚΞΝ ἡμικύκλια· ἐπὶ γὰρ ἴσων εἰσὶ διαμέτρων τῶν ΒΔ, ΚΝ· ἴσα ἐστὶ καὶ τὰ ΒΕ, ΒΞ, ΚΞ τεταρτημόρια ἀλλήλοις. ὅσαι ἄρα εἰσὶν ἐν τῷ ΒΕ τεταρτημορίῳ πλευραὶ τοῦ πολυγώνου, τοσαῦταί εἰσι καὶ ἐν τοῖς ΒΞ, ΚΞ τεταρτημορίοις ἴσαι ταῖς ΒΚ, ΚΛ, ΛΜ, ΜΕ εὐθείαις. ἐγγεγράφθωσαν καὶ ἔστωσαν αἱ ΒΟ, ΟΠ, ΠΡ, ΡΞ, ΚΣ, ΣΤ, ΤΥ, ΥΞ, καὶ ἐπεζεύχθωσαν αἱ ΣΟ, ΤΠ, ΥΡ, καὶ ἀπὸ τῶν Ο, Σ ἐπὶ τὸ τοῦ ΒΓΔΕ κύκλου ἐπίπεδον κάθετοι ἤχθωσαν· πεσοῦνται δὴ ἐπὶ τὰς κοινὰς τομὰς τῶν ἐπιπέδων τὰς ΒΔ, ΚΝ, ἐπειδήπερ καὶ τὰ τῶν ΒΞΔ, ΚΞΝ ἐπίπεδα ὀρθά ἐστι πρὸς τὸ τοῦ ΒΓΔΕ κύκλου ἐπίπεδον. πιπτέτωσαν, καὶ ἔστωσαν αἱ ΟΦ, ΣΧ, καὶ ἐπεζεύχθω ἡ ΧΦ. καὶ ἐπεὶ ἐν ἴσοις ἡμικυκλίοις τοῖς ΒΞΔ, ΚΞΝ ἴσαι ἀπειλημμέναι εἰσὶν αἱ ΒΟ, ΚΣ, καὶ κάθετοι ἠγμέναι εἰσὶν αἱ ΟΦ, ΣΧ, ἴση [ἄρα] ἐστὶν ἡ μὲν ΟΦ τῇ ΣΧ, ἡ δὲ ΒΦ τῇ ΚΧ. ἔστι δὲ καὶ ὅλη ἡ ΒΑ ὅλῃ τῇ ΚΑ ἴση· καὶ λοιπὴ ἄρα ἡ ΦΑ λοιπῇ τῇ ΧΑ ἐστιν ἴση· ἔστιν ἄρα ὡς ἡ ΒΦ πρὸς τὴν ΦΑ, οὕτως ἡ ΚΧ πρὸς τὴν ΧΑ· παράλληλος ἄρα ἐστὶν ἡ ΧΦ τῇ ΚΒ. καὶ ἐπεὶ ἑκατέρα τῶν ΟΦ, ΣΧ ὀρθή ἐστι πρὸς τὸ τοῦ ΒΓΔΕ κύκλου ἐπίπεδον, παράλληλος ἄρα ἐστὶν ἡ ΟΦ τῇ ΣΧ. ἐδείχθη δὲ αὐτῇ καὶ ἴση· καὶ αἱ ΧΦ, ΣΟ ἄρα ἴσαι εἰσὶ καὶ παράλληλοι. καὶ ἐπεὶ παράλληλός ἐστιν ἡ ΧΦ τῇ ΣΟ, ἀλλὰ ἡ ΧΦ τῇ ΚΒ ἐστι παράλληλος, καὶ ἡ ΣΟ ἄρα τῇ ΚΒ ἐστι παράλληλος. καὶ ἐπιζευγνύουσιν αὐτὰς αἱ ΒΟ, ΚΣ· τὸ ΚΒΟΣ ἄρα τετράπλευρον ἐν ἑνί ἐστιν ἐπιπέδῳ, ἐπειδήπερ, ἐὰν ὦσι δύο εὐθεῖαι παράλληλοι, καὶ ἐφ' ἑκατέρας αὐτῶν ληφθῇ τυχόντα σημεῖα, ἡ ἐπὶ τὰ σημεῖα ἐπιζευγνυμένη εὐθεῖα ἐν τῷ αὐτῷ ἐπιπέδῳ ἐστὶ ταῖς παραλλήλοις. διὰ τὰ αὐτὰ δὴ καὶ ἑκάτερον τῶν ΣΟΠΤ, ΤΠΡΥ τετραπλεύρων ἐν ἑνί ἐστιν ἐπιπέδῳ. ἔστι δὲ καὶ τὸ ΥΡΞ τρίγωνον ἐν ἑνὶ ἐπιπέδῳ. ἐὰν δὴ νοήσωμεν ἀπὸ τῶν Ο, Σ, Π, Τ, Ρ, Υ σημείων ἐπὶ τὸ Α ἐπιζευγνυμένας εὐθείας, συσταθήσεταί τι σχῆμα στερεὸν πολύεδρον μεταξὺ τῶν ΒΞ, ΚΞ περιφερειῶν ἐκ πυραμίδων συγκείμενον, ὧν βάσεις μὲν τὰ ΚΒΟΣ, ΣΟΠΤ, ΤΠΡΥ τετράπλευρα καὶ τὸ ΥΡΞ τρίγωνον, κορυφὴ δὲ τὸ Α σημεῖον. ἐὰν δὲ καὶ ἐπὶ ἑκάστης τῶν ΚΛ, ΛΜ, ΜΕ πλευρῶν καθάπερ ἐπὶ τῆς ΒΚ τὰ αὐτὰ κατασκευάσωμεν καὶ ἔτι ἐπὶ τῶν λοιπῶν τριῶν τεταρτημορίων, συσταθήσεταί τι σχῆμα πολύεδρον ἐγγεγραμμένον εἰς τὴν σφαῖραν πυραμίσι περιεχόμενον, ὧν βάσεις [μὲν] τὰ εἰρημένα τετράπλευρα καὶ τὸ ΥΡΞ τρίγωνον καὶ τὰ ὁμοταγῆ αὐτοῖς, κορυφὴ δὲ τὸ Α σημεῖον.
Λέγω, ὅτι τὸ εἰρημένον πολύεδρον οὐκ ἐφάψεται τῆς ἐλάσσονος σφαίρας κατὰ τὴν ἐπιφάνειαν, ἐφ' ἧς ἐστιν ὁ ΖΗΘ κύκλος.
Ἤχθω ἀπὸ τοῦ Α σημείου ἐπὶ τὸ τοῦ ΚΒΟΣ τετραπλεύρου ἐπίπεδον κάθετος ἡ ΑΨ καὶ συμβαλλέτω τῷ ἐπιπέδῳ κατὰ τὸ Ψ σημεῖον, καὶ ἐπεζεύχθωσαν αἱ ΨΒ, ΨΚ. καὶ ἐπεὶ ἡ ΑΨ ὀρθή ἐστι πρὸς τὸ τοῦ ΚΒΟΣ τετραπλεύρου ἐπίπεδον, καὶ πρὸς πάσας ἄρα τὰς ἁπτομένας αὐτῆς εὐθείας καὶ οὔσας ἐν τῷ τοῦ τετραπλεύρου ἐπιπέδῳ ὀρθή ἐστιν. ἡ ΑΨ ἄρα ὀρθή ἐστι πρὸς ἑκατέραν τῶν ΒΨ, ΨΚ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΒ τῇ ΑΚ, ἴσον ἐστὶ καὶ τὸ ἀπὸ τῆς ΑΒ τῷ ἀπὸ τῆς ΑΚ. καί ἐστι τῷ μὲν ἀπὸ τῆς ΑΒ ἴσα τὰ ἀπὸ τῶν ΑΨ, ΨΒ· ὀρθὴ γὰρ ἡ πρὸς τῷ Ψ· τῷ δὲ ἀπὸ τῆς ΑΚ ἴσα τὰ ἀπὸ τῶν ΑΨ, ΨΚ. τὰ ἄρα ἀπὸ τῶν ΑΨ, ΨΒ ἴσα ἐστὶ τοῖς ἀπὸ τῶν ΑΨ, ΨΚ. κοινὸν ἀφῃρήσθω τὸ ἀπὸ τῆς ΑΨ· λοιπὸν ἄρα τὸ ἀπὸ τῆς ΒΨ λοιπῷ τῷ ἀπὸ τῆς ΨΚ ἴσον ἐστίν· ἴση ἄρα ἡ ΒΨ τῇ ΨΚ. ὁμοίως δὴ δείξομεν, ὅτι καὶ αἱ ἀπὸ τοῦ Ψ ἐπὶ τὰ Ο, Σ ἐπιζευγνύμεναι εὐθεῖαι ἴσαι εἰσὶν ἑκατέρᾳ τῶν ΒΨ, ΨΚ. ὁ ἄρα κέντρῳ τῷ Ψ καὶ διαστήματι ἑνὶ τῶν ΨΒ, ΨΚ γραφόμενος κύκλος ἥξει καὶ διὰ τῶν Ο, Σ, καὶ ἔσται ἐν κύκλῳ τὸ ΚΒΟΣ τετράπλευρον.
Καὶ ἐπεὶ μείζων ἐστὶν ἡ ΚΒ τῆς ΧΦ, ἴση δὲ ἡ ΧΦ τῇ ΣΟ, μείζων ἄρα ἡ ΚΒ τῆς ΣΟ. ἴση δὲ ἡ ΚΒ ἑκατέρᾳ τῶν ΚΣ, ΒΟ· καὶ ἑκατέρα ἄρα τῶν ΚΣ, ΒΟ τῆς ΣΟ μείζων ἐστίν. καὶ ἐπεὶ ἐν κύκλῳ τετράπλευρόν ἐστι τὸ ΚΒΟΣ, καὶ ἴσαι αἱ ΚΒ, ΒΟ, ΚΣ, καὶ ἐλάττων ἡ ΟΣ, καὶ ἐκ τοῦ κέντρου τοῦ κύκλου ἐστὶν ἡ ΒΨ, τὸ ἄρα ἀπὸ τῆς ΚΒ τοῦ ἀπὸ τῆς ΒΨ μεῖζόν ἐστιν ἢ διπλάσιον. ἤχθω ἀπὸ τοῦ Κ ἐπὶ τὴν ΒΦ κάθετος ἡ ΚΩ. καὶ ἐπεὶ ἡ ΒΔ τῆς ΔΩ ἐλάττων ἐστὶν ἢ διπλῆ, καί ἐστιν ὡς ἡ ΒΔ πρὸς τὴν ΔΩ, οὕτως τὸ ὑπὸ τῶν ΔΒ, ΒΩ πρὸς τὸ ὑπὸ [τῶν] ΔΩ, ΩΒ, ἀναγραφομένου ἀπὸ τῆς ΒΩ τετραγώνου καὶ συμπληρουμένου τοῦ ἐπὶ τῆς ΩΔ παραλληλογράμμου καὶ τὸ ὑπὸ ΔΒ, ΒΩ ἄρα τοῦ ὑπὸ ΔΩ, ΩΒ ἔλαττόν ἐστιν ἢ διπλάσιον. καί ἐστι τῆς ΚΔ ἐπιζευγνυμένης τὸ μὲν ὑπὸ ΔΒ, ΒΩ ἴσον τῷ ἀπὸ τῆς ΒΚ, τὸ δὲ ὑπὸ τῶν ΔΩ, ΩΒ ἴσον τῷ ἀπὸ τῆς ΚΩ· τὸ ἄρα ἀπὸ τῆς ΚΒ τοῦ ἀπὸ τῆς ΚΩ ἔλασσόν ἐστιν ἢ διπλάσιον. ἀλλὰ τὸ ἀπὸ τῆς ΚΒ τοῦ ἀπὸ τῆς ΒΨ μεῖζόν ἐστιν ἢ διπλάσιον· μεῖζον ἄρα τὸ ἀπὸ τῆς ΚΩ τοῦ ἀπὸ τῆς ΒΨ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΒΑ τῇ ΚΑ, ἴσον ἐστὶ τὸ ἀπὸ τῆς ΒΑ τῷ ἀπὸ τῆς ΑΚ. καί ἐστι τῷ μὲν ἀπὸ τῆς ΒΑ ἴσα τὰ ἀπὸ τῶν ΒΨ, ΨΑ, τῷ δὲ ἀπὸ τῆς ΚΑ ἴσα τὰ ἀπὸ τῶν ΚΩ, ΩΑ· τὰ ἄρα ἀπὸ τῶν ΒΨ, ΨΑ ἴσα ἐστὶ τοῖς ἀπὸ τῶν ΚΩ, ΩΑ, ὧν τὸ ἀπὸ τῆς ΚΩ μεῖζον τοῦ ἀπὸ τῆς ΒΨ· λοιπὸν ἄρα τὸ ἀπὸ τῆς ΩΑ ἔλασσόν ἐστι τοῦ ἀπὸ τῆς ΨΑ. μείζων ἄρα ἡ ΑΨ τῆς ΑΩ· πολλῷ ἄρα ἡ ΑΨ μείζων ἐστὶ τῆς ΑΗ. καί ἐστιν ἡ μὲν ΑΨ ἐπὶ μίαν τοῦ πολυέδρου βάσιν, ἡ δὲ ΑΗ ἐπὶ τὴν τῆς ἐλάσσονος σφαίρας ἐπιφάνειαν· ὥστε τὸ πολύεδρον οὐ ψαύσει τῆς ἐλάσσονος σφαίρας κατὰ τὴν ἐπιφάνειαν.
Δύο ἄρα σφαιρῶν περὶ τὸ αὐτὸ κέντρον οὐσῶν εἰς τὴν μείζονα σφαῖραν στερεὸν πολύεδρον ἐγγέγραπται μὴ ψαῦον τῆς ἐλάσσονος σφαίρας κατὰ τὴν ἐπιφάνειαν· ὅπερ ἔδει ποιῆσαι.
Ἐὰν δὲ καὶ εἰς ἑτέραν σφαῖραν τῷ ἐν τῇ ΒΓΔΕ σφαίρᾳ στερεῷ πολυέδρῳ ὅμοιον στερεὸν πολύεδρον ἐγγραφῇ, τὸ ἐν τῇ ΒΓΔΕ σφαίρᾳ στερεὸν πολύεδρον πρὸς τὸ ἐν τῇ ἑτέρᾳ σφαίρᾳ στερεὸν πολύεδρον τριπλασίονα λόγον ἔχει, ἤπερ ἡ τῆς ΒΓΔΕ σφαίρας διάμετρος πρὸς τὴν τῆς ἑτέρας σφαίρας διάμετρον. διαιρεθέντων γὰρ τῶν στερεῶν εἰς τὰς ὁμοιοπληθεῖς καὶ ὁμοιοταγεῖς πυραμίδας ἔσονται αἱ πυραμίδες ὅμοιαι. αἱ δὲ ὅμοιαι πυραμίδες πρὸς ἀλλήλας ἐν τριπλασίονι λόγῳ εἰσὶ τῶν ὁμολόγων πλευρῶν· ἡ ἄρα πυραμίς, ἧς βάσις μέν ἐστι τὸ ΚΒΟΣ τετράπλευρον, κορυφὴ δὲ τὸ Α σημεῖον, πρὸς τὴν ἐν τῇ ἑτέρᾳ σφαίρᾳ ὁμοιοταγῆ πυραμίδα τριπλασίονα λόγον ἔχει, ἤπερ ἡ ὁμόλογος πλευρὰ πρὸς τὴν ὁμόλογον πλευράν, τουτέστιν ἤπερ ἡ ΑΒ ἐκ τοῦ κέντρου τῆς σφαίρας τῆς περὶ κέντρον τὸ Α πρὸς τὴν ἐκ τοῦ κέντρου τῆς ἑτέρας σφαίρας. ὁμοίως καὶ ἑκάστη πυραμὶς τῶν ἐν τῇ περὶ κέντρον τὸ Α σφαίρᾳ πρὸς ἑκάστην ὁμοταγῆ πυραμίδα τῶν ἐν τῇ ἑτέρᾳ σφαίρᾳ τριπλασίονα λόγον ἕξει, ἤπερ ἡ ΑΒ πρὸς τὴν ἐκ τοῦ κέντρου τῆς ἑτέρας σφαίρας. καὶ ὡς ἓν τῶν ἡγουμένων πρὸς ἓν τῶν ἑπομένων, οὕτως ἅπαντα τὰ ἡγούμενα πρὸς ἅπαντα τὰ ἑπόμενα· ὥστε ὅλον τὸ ἐν τῇ περὶ κέντρον τὸ Α σφαίρᾳ στερεὸν πολύεδρον πρὸς ὅλον τὸ ἐν τῇ ἑτέρᾳ [σφαίρᾳ] στερεὸν πολύεδρον τριπλασίονα λόγον ἕξει, ἤπερ ἡ ΑΒ πρὸς τὴν ἐκ τοῦ κέντρου τῆς ἑτέρας σφαίρας, τουτέστιν ἤπερ ἡ ΒΔ διάμετρος πρὸς τὴν τῆς ἑτέρας σφαίρας διάμετρον· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ιβ΄.
Περιεχόμενα Στοιχείων Εὐκλείδου
Copyright©1999 Dimitrios E. Mourmouras