Στοιχεία Εὐκλείδου ι΄
[Βιβλίον X]
Αἱ Προτάσεις τῶν Στοιχείων ι΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις κα΄. [21]
Τὸ ὑπὸ ῥητῶν δυνάμει μόνον συμμέτρων εὐθειῶν περιεχόμενον ὀρθογώνιον ἄλογόν ἐστιν, καὶ ἡ δυναμένη αὐτὸ ἄλογός ἐστιν, καλείσθω δὲ μέση.
Ὑπὸ γὰρ ῥητῶν δυνάμει μόνον συμμέτρων εὐθειῶν τῶν ΑΒ, ΒΓ ὀρθογώνιον περιεχέσθω τὸ ΑΓ· λέγω, ὅτι ἄλογόν ἐστι τὸ ΑΓ, καὶ ἡ δυναμένη αὐτὸ ἄλογός ἐστιν, καλείσθω δὲ μέση.
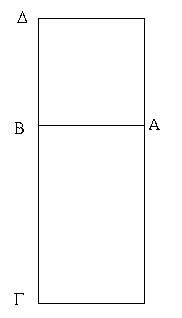
Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΑΒ τετράγωνον τὸ ΑΔ· ῥητὸν ἄρα ἐστὶ τὸ ΑΔ. καὶ ἐπεὶ ἀσύμμετρός ἐστιν ἡ ΑΒ τῇ ΒΓ μήκει· δυνάμει γὰρ μόνον ὑπόκεινται σύμμετροι· ἴση δὲ ἡ ΑΒ τῇ ΒΔ, ἀσύμμετρος ἄρα ἐστὶ καὶ ἡ ΔΒ τῇ ΒΓ μήκει. καί ἐστιν ὡς ἡ ΔΒ πρὸς τὴν ΒΓ, οὕτως τὸ ΑΔ πρὸς τὸ ΑΓ· ἀσύμμετρον ἄρα [ἐστὶ] τὸ ΔΑ τῷ ΑΓ. ῥητὸν δὲ τὸ ΔΑ· ἄλογον ἄρα ἐστὶ τὸ ΑΓ· ὥστε καὶ ἡ δυναμένη τὸ ΑΓ [τουτέστιν ἡ ἴσον αὐτῷ τετράγωνον δυναμένη] ἄλογός ἐστιν, καλείσθω δὲ μέση· ὅπερ ἔδει δεῖξαι.
Ἐὰν ὦσι δύο εὐθεῖαι, ἔστιν ὡς ἡ πρώτη πρὸς τὴν δευτέραν, οὕτως τὸ ἀπὸ τῆς πρώτης πρὸς τὸ ὑπὸ τῶν δύο εὐθειῶν.
Ἔστωσαν δύο εὐθεῖαι αἱ ΖΕ, ΕΗ. λέγω, ὅτι ἐστὶν ὡς ἡ ΖΕ πρὸς τὴν ΕΗ, οὕτως τὸ ἀπὸ τῆς ΖΕ πρὸς τὸ ὑπὸ τῶν ΖΕ, ΕΗ.
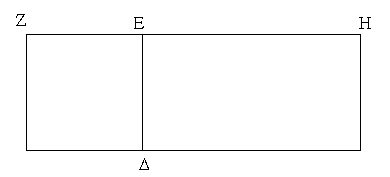
Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΖΕ τετράγωνον τὸ ΔΖ, καὶ συμπεπληρώσθω τὸ ΗΔ. ἐπεὶ οὖν ἐστιν ὡς ἡ ΖΕ πρὸς τὴν ΕΗ, οὕτως τὸ ΖΔ πρὸς τὸ ΔΗ, καί ἐστι τὸ μὲν ΖΔ τὸ ἀπὸ τῆς ΖΕ, τὸ δὲ ΔΗ τὸ ὑπὸ τῶν ΔΕ, ΕΗ, τουτέστι τὸ ὑπὸ τῶν ΖΕ, ΕΗ, ἔστιν ἄρα ὡς ἡ ΖΕ τὴν ΕΗ, οὕτως τὸ ἀπὸ τῆς ΖΕ πρὸς τὸ ὑπὸ τῶν ΖΕ, ΕΗ. ὁμοίως δὲ καὶ ὡς τὸ ὑπὸ τῶν ΗΕ, ΕΖ πρὸς τὸ ἀπὸ τῆς ΕΖ, τουτέστιν ὡς τὸ ΗΔ πρὸς τὸ ΖΔ, οὕτως ἡ ΗΕ πρὸς τὴν ΕΖ· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ι΄.
Περιεχόμενα Στοιχείων Εὐκλείδου
Copyright©1999 Dimitrios E. Mourmouras