Στοιχεία Εὐκλείδου ι΄
[Βιβλίον X]
Αἱ Προτάσεις τῶν Στοιχείων ι΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις ις΄. [16]
Ἐὰν δύο μεγέθη ἀσύμμετρα συντεθῇ, καὶ τὸ ὅλον ἑκατέρῳ αὐτῶν ἀσύμμετρον ἔσται· κἂν τὸ ὅλον ἑνὶ αὐτῶν ἀσύμμετρον ᾖ, καὶ τὰ ἐξ ἀρχῆς μεγέθη ἀσύμμετρα ἔσται.
Συγκείσθω γὰρ δύο μεγέθη ἀσύμμετρα τὰ ΑΒ, ΒΓ· λέγω, ὅτι καὶ ὅλον τὸ ΑΓ ἑκατέρῳ τῶν ΑΒ, ΒΓ ἀσύμμετρόν ἐστιν.
Εἰ γὰρ μή ἐστιν ἀσύμμετρα τὰ ΓΑ, ΑΒ, μετρήσει τι [αὐτὰ] μέγεθος. μετρείτω, εἰ δυνατόν, καὶ ἔστω τὸ Δ. ἐπεὶ οὖν τὸ Δ τὰ ΓΑ, ΑΒ μετρεῖ, καὶ λοιπὸν ἄρα τὸ ΒΓ μετρήσει. μετρεῖ δὲ καὶ τὸ ΑΒ· τὸ Δ ἄρα τὰ ΑΒ, ΒΓ μετρεῖ. σύμμετρα ἄρα ἐστὶ τὰ ΑΒ, ΒΓ· ὑπέκειντο δὲ καὶ ἀσύμμετρα· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα τὰ ΓΑ, ΑΒ μετρήσει τι μέγεθος· ἀσύμμετρα ἄρα ἐστὶ τὰ ΓΑ, ΑΒ. ὁμοίως δὴ δείξομεν, ὅτι καὶ τὰ ΑΓ, ΓΒ ἀσύμμετρά ἐστιν. τὸ ΑΓ ἄρα ἑκατέρῳ τῶν ΑΒ, ΒΓ ἀσύμμετρόν ἐστιν.
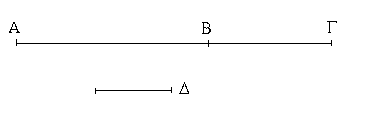
Ἀλλὰ δὴ τὸ ΑΓ ἑνὶ τῶν ΑΒ, ΒΓ ἀσύμμετρον ἔστω. ἔστω δὴ πρότερον τῷ ΑΒ· λέγω, ὅτι καὶ τὰ ΑΒ, ΒΓ ἀσύμμετρά ἐστιν. εἰ γὰρ ἔσται σύμμετρα, μετρήσει τι αὐτὰ μέγεθος. μετρείτω, καὶ ἔστω τὸ Δ. ἐπεὶ οὖν τὸ Δ τὰ ΑΒ, ΒΓ μετρεῖ, καὶ ὅλον ἄρα τὸ ΑΓ μετρήσει. μετρεῖ δὲ καὶ τὸ ΑΒ· τὸ Δ ἄρα τὰ ΓΑ, ΑΒ μετρεῖ. σύμμετρα ἄρα ἐστὶ τὰ ΓΑ, ΑΒ· ὑπέκειτο δὲ καὶ ἀσύμμετρα· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα τὰ ΑΒ, ΒΓ μετρήσει τι μέγεθος· ἀσύμμετρα ἄρα ἐστὶ τὰ ΑΒ, ΒΓ.
Ἐὰν ἄρα δύο μεγέθη, καὶ τὰ ἑξῆς.
Ἐὰν παρά τινα εὐθεῖαν παραβληθῇ παραλληλόγραμμον ἐλλεῖπον εἴδει τετραγώνῳ, τὸ παραβληθὲν ἴσον ἐστὶ τῷ ὑπὸ τῶν ἐκ τῆς παραβολῆς γενομένων τμημάτων τῆς εὐθείας.
Παρὰ γὰρ εὐθεῖαν τὴν ΑΒ παραβεβλήσθω παραλληλόγραμμον τὸ ΑΔ ἐλλεῖπον εἴδει τετραγώνῳ τῷ ΔΒ· λέγω, ὅτι ἴσον ἐστὶ τὸ ΑΔ τῷ ὑπὸ τῶν ΑΓ, ΓΒ.
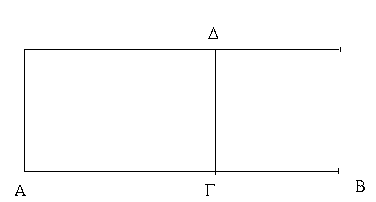
Καί ἐστιν αὐτόθεν φανερόν· ἐπεὶ γὰρ τετράγωνόν ἐστι τὸ ΔΒ, ἴση ἐστὶν ἡ ΔΓ τῇ ΓΒ, καί ἐστι τὸ ΑΔ τὸ ὑπὸ τῶν ΑΓ, ΓΔ, τουτέστι τὸ ὑπὸ τῶν ΑΓ, ΓΒ.
Ἐὰν ἄρα παρά τινα εὐθεῖαν, καὶ τὰ ἑξῆς.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ι΄.
Περιεχόμενα Στοιχείων Εὐκλείδου
Copyright©1999 Dimitrios E. Mourmouras